Question

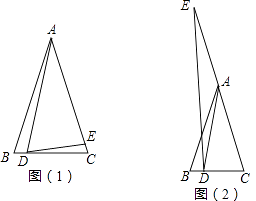
【题目】如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B=90°，AB=8，DH=3，平移距离为4，求阴影部分的面积为（ ）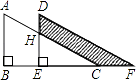
A.20
B.24
C.25
D.26

Answer 1

【答案】D
【解析】解：∵平移距离为4， ∴BE=4，
∵AB=8，DH=3，
∴EH=8﹣3=5，
∵△HEC～△ABC，
∴ = = ，
∴ = ，
解得CE= ，
∴阴影部分的面积为：
S△DEF﹣S△HEC
=8×（ +4）÷2﹣ ×5÷2
= ﹣
=26
故选：D．
【考点精析】本题主要考查了平移的性质的相关知识点，需要掌握①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等才能正确解答此题．