题目内容
【题目】已知,矩形ABCD中,AB=4cm,AD=2AB,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.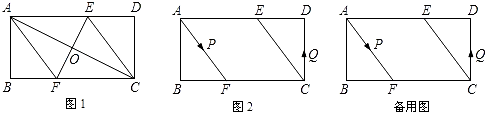
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒.当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值;
②若点P、Q的速度分别为v1、v2(cm/s),点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,试探究a与b满足的数量关系.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE.
∵EF垂直平分AC,
∴OA=OC.
∵在△AOE和△COF中,
 ,
,
∴△AOE≌△COF(AAS),
∴OE=OF.
∵EF⊥AC,
∴四边形AFCE为菱形.
设菱形的边长AF=CF=xcm,则BF=(8﹣x)cm,
在Rt△ABF中,AB=4cm,由勾股定理得:AB2+BF2=AF2,
即42+(8﹣x)2=x2,
解得:x=5,
∴AF=5
(2)
①解:根据题意得,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形;
同理P点AB上时,Q点DE或CE上,也不能构成平行四边形.
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12﹣4t,
∴5t=12﹣4t,
解得:t= ![]() ,
,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t= ![]() 秒;
秒;
②由①得,PC=QA时,以A,C,P,Q四点为顶点的四边形是平行四边形,
设运动时间为y秒,
则yv1=12﹣yv2,
解得,y= ![]() ,
,
∴a= ![]() ×v1,b=
×v1,b= ![]() ×v2,
×v2,
∴ ![]() =
= ![]() .
.

【解析】(1)先证明四边形ABCD为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定,根据勾股定理即可求AF的长;(2)①分情况讨论可知,P点在BF上,Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;②由①的结论用v1、v2表示出A、C、P、Q四点为顶点的四边形是平行四边形时所需的时间,计算即可.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对平行四边形的判定的理解,了解两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.