Question

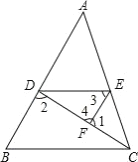
【题目】如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，∠B=60°，AB=10，BC=4，点P沿线段AB从点A向点B运动，设AP=x．

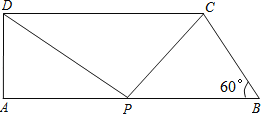
（1）求AD的长；

（2）点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由．

Answer 1

【答案】（1）2；（2）存在，x=2

【解析】

试题分析：（1）过C作CE⊥AB于点E，在△CEB中可求得CE，即可求得AD的长；

（2）因为△APD为直角三角形，所以△PBC也为直角三角形，分∠PCB=90°和∠CPB=90°两种情况进行讨论求解即可．

解：（1）如图，过C作CE⊥AB于点E，

则四边形AECD为矩形，

∴AD=CE，

在Rt△BEC中，BC=4，∠B=60°，

∴CE=BCsin60°=4×=2；

（2）存在．

若以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似，则△PCB必有一个角是直角．

①当∠PCB=90°时，

在Rt△BCP中，∠B=60°，BC=4，

可求得BP=8，此时AP=2，

在Rt△ADP中，由勾股定理可求得PD=4，

∴=，=，

∴=，且∠DAP=∠PCB，

∴△ADP∽△CPB，

此时AP=x=2；

②当∠CPB=90°时，P点即为E点位置，此时BP=2，AP=8，即

∵==，=，

∴≠，

∴△PCB与△ADP不相似，

综上可知当x=2时，△ADP∽△CPB．