��Ŀ����
����Ŀ���ס�����̨�������ӹ�һ��������ڼӹ���������̨�������ı���һ�ι���Ч�ʣ��ӹ�����ʼ���ӹ������������̨����ǡ��ͬʱ����6Сʱ���ס�����̨�������Լӹ����������y��������ӹ�ʱ��x��ʱ��֮��ĺ���ͼ��ֱ�Ϊ����OA��AB������OC��CD����ͼ��ʾ��
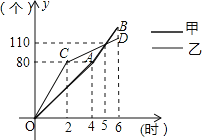
��1�������ı乤��Ч��ǰÿСʱ�ӹ���� ����
��2�����һ����ı乤��Ч�ʺ�y��x֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��3��������������ܸ�����
��4��ֱ��д�����ס�����̨�������ӹ���������10��ʱ��x��ֵΪ ��
���𰸡���1��20����2��y��=10x+60��2��x��6������3��260����4��![]() ��
��
���������⣺��1��80��4=20��������
�ʴ�Ϊ��20��
��2����ͼ���C��2��80����D��5��110����
�������ʽΪy=kx+b��k��0����
��![]() ����ã�
����ã�![]() ��
��
��y��=10x+60��2��x��6����
��3����AB����4��80������5��110����
����AB�Ľ���ʽΪy��=mx+n��m��0����
��![]() ����ã�
����ã�![]() ��
��
��y��=30x��40��4��x��6����
��x=6ʱ��y��=30��6��40=140��y��=10��6+60=120��
������������ܸ�����140+120=260��
��4��40x��10=20x��
��ã�x=![]() ��
��
10x+60��10=30x��40��
��ã�x=![]() ��
��
30x��40��10=10x+60��
��ã�x=![]() ��
��
���ס�����̨�������ӹ���������10��ʱ��x��ֵΪ![]() ��
��
�ʴ�Ϊ��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�