题目内容
【题目】某商店需要购进甲、乙两种商品共130件,其进价和获利情况如下表:

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于3000元,且销售完这批商品后总获利多于1048元,请问有哪些购货方案?
【答案】(1)甲种商品购进50件,乙种商品购进80件;(2)有两种购货方案:方案一:甲种商品购进61件,乙种商品购进69件;方案二:甲种商品购进62件,乙种商品购进68件.
【解析】
(1)设甲种商品应购进x件,乙种商品应购进y件,根据购进甲、乙两种商品共130件且销售完这批商品后能获利1100元,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设甲种商品购进a件,则乙种商品购进(130-a)件,根据购货资金少于3000元且销售完这批商品后获利多于1048元,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,取其内的整数即可得出各购货方案.
(1)设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:![]() ,
,
解得:![]() .
.
答:甲种商品购进50件,乙种商品购进80件.
(2)设甲种商品购进a件,则乙种商品购进(130-a)件.
根据题意得: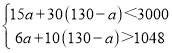 ,
,
解得:60<a<63.
∵a为非负整数,
∴a取61,62,
∴130-a相应取69,68.
答:有两种购货方案:方案一:甲种商品购进61件,乙种商品购进69件;方案二:甲种商品购进62件,乙种商品购进68件.

练习册系列答案
相关题目