题目内容
【题目】如图,∠OAB=45°,点A的坐标是(4,0),AB= ![]() ,连结OB.
,连结OB.
(1)直接写出点B的坐标.
(2)动点P从点O出发,沿折线O﹣B﹣A方向向终点A匀速运动,另一动点Q从点O出发,沿OA方向匀速运动,若点P的运动速度为 ![]() 个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
(3)动点P仍按(2)中的方向和速度运动,但Q点从A点向O点运动,速度为1个单位/秒,P、Q与△OAB中的任意一个顶点形成直角三角形时,求此时t(t≠0)的值.
【答案】
(1)
解:过B作BC⊥OA于C,
∵∠OAB=45°,
∴△ACB为等腰直角三角形,
∵AB=2 ![]() ,
,
∴BC=AC=2,
∵A(4,0),
∴OA=4,
∴OC=OA﹣AC=4﹣2=2,
∴B(2,2)
(2)
解:过P作PD⊥OA于D,
如图1,
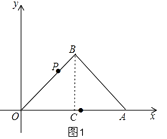
由(1)得:OC=BC=2,∠BCO=90°,
∴∠AOB=45°,
如图2,
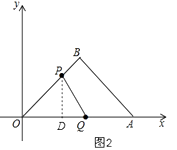
由题意得:OP= ![]() t,OQ=t,
t,OQ=t,
∵△POD是等腰直角三角形,
∴PD= ![]() =t,
=t,
∵S△OPQ=1.5,
∴ ![]() OQPD=1.5,
OQPD=1.5,
![]() t2=1.5,
t2=1.5,
t= ![]() ,
,
答:当t= ![]() 时,△OPQ的面积等于1.5
时,△OPQ的面积等于1.5
(3)
解:分四种情况:
①当0<t≤2时,∠OPQ=90°,如图3,
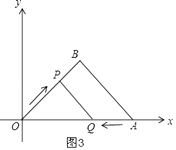
由题意得:OP= ![]() t,AQ=t,OQ=4﹣t,
t,AQ=t,OQ=4﹣t,
则cos45°= ![]() ,
,
![]() =
= ![]() ,
,
解得:t= ![]() ;
;
②当0<t≤2时,∠OQP=90°,如图4,

由题意得:OP= ![]() t,AQ=t,OQ=4﹣t,
t,AQ=t,OQ=4﹣t,
则cos45°= ![]() ,
,
![]() =
= ![]() ,
,
解得:t=2;
③当2<t<4时,AQ=t,AP=4 ![]() ﹣
﹣ ![]() t,
t,
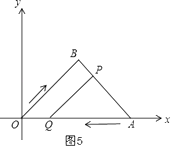
当∠APQ=90°时,如图5,
cos45°= ![]() ,
,
![]() =
= ![]() ,
,
解得:t= ![]() ;
;
④如图6,点Q与O重合,点P与A重合,

∠PBQ=90°,此时t=4;
综上所述,P、Q与△OAB中的任意一个顶点形成直角三角形时,t的值为 ![]() 或2或
或2或 ![]() 或4.
或4.
【解析】(1)如图1,过B作BC⊥OA于C,根据∠OAB=45°,可知△ACB为等腰直角三角形,求出BC和AC的长为2,再由点A的坐标得出OA=4,所以得出B(2,2);(2)如图2,作△OPQ的高线PD,根据速度和时间表示动点的路程:OP= ![]() t,OQ=t,根据图1求出∠AOB=45°,所以△POD是等腰直角三角形,表示出高线PD的长,代入面积公式列等量关系式可求得结论;(3)分四种情况进行讨论:①当0<t≤2时,∠OPQ=90°,如图3,②当0<t≤2时,∠OQP=90°,如图4,③当2<t<4时,∠APQ=90°,如图5,④点Q与O重合,点P与A重合,如图6;分别根据45°的余弦列式求出.
t,OQ=t,根据图1求出∠AOB=45°,所以△POD是等腰直角三角形,表示出高线PD的长,代入面积公式列等量关系式可求得结论;(3)分四种情况进行讨论:①当0<t≤2时,∠OPQ=90°,如图3,②当0<t≤2时,∠OQP=90°,如图4,③当2<t<4时,∠APQ=90°,如图5,④点Q与O重合,点P与A重合,如图6;分别根据45°的余弦列式求出.
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.

 53随堂测系列答案
53随堂测系列答案