题目内容
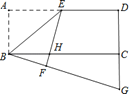
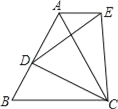
【题目】如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
【答案】(1)根据等边三角形的性质可得∠ACB=∠DCE=60°,AC=BC,DC=EC,再由∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD可得∠BCD=∠ACE,即可证得结论;
(2)根据全等三角形的性质可得∠ABC=∠CAE=60°,再结合∠ACB=60°可得∠CAE=∠ACB,从而证得结论.
【解析】
试题(1)∵△ABC与△EDC是等边三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=EC
又∵∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD,
∴∠BCD=∠ACE.
∴△ACE≌△BCD(SAS);
(2)∵ACE≌△BCD,
∴∠ABC=∠CAE=60°
又∵∠ACB=60°,
∴∠CAE=∠ACB
∴ AE∥BC.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目