题目内容
【题目】在平面直角坐标系中,点A(0,m)和点B(n,0)分别在y轴和x轴的正半轴上,满足![]() ,连接线段AB,点C为AB上一动点.
,连接线段AB,点C为AB上一动点.
(1)填空:m=_____,n=_____;
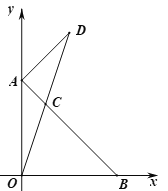
(2)如图,连接OC并延长至点D,使得DC=OC,连接AD.若△AOC的面积为2,求点D的坐标;
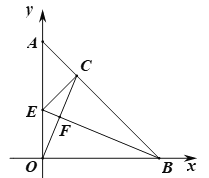
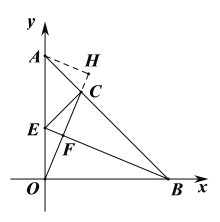
(3)如图,BC=OB,∠ABO的平分线交线段AO于点E,交线段OC于点F,连接EC.
求证:①△ACE为等腰直角三角形;
②BF-EF=OC.
【答案】(1)4,4;(2)D(2,6);(3)①见解析;②见解析.
【解析】
(1)根据非负数的性质可得关于m、n的方程组,解方程组即可求出m、n的值;
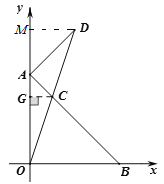
(2)过点C作CG⊥y轴于点G,过点D作DM⊥y轴于点M,如图,由题意易得△AOB和△ACG均为等腰直角三角形,由△AOC的面积为2可求得AG的长,进而可求出OG的长,再利用三角形的中位线可得DM和OM的长,即得点D的坐标;
(3)①先利用SAS证明△OBE≌△CBE,可得∠BCE=∠BOA=90°,再根据∠OAB =45°和三角形的内角和求出∠AEC的度数,进一步即可证得结论;
②过点A作AH⊥OC交OC的延长线于点H,如图,根据AAS可证明△ACH≌△CEF,从而得EF=CH,同理可证△AOH≌△OBF,得OH=BF,问题即得解决.
解:(1)∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
故答案为4,4;
(2)由(1)得,A(0,4)、B(4,0),∴OA=OB=4,∵∠BOA=90°,∴∠OAB=∠OBA=45°,
过点C作CG⊥y轴于点G,过点D作DM⊥y轴于点M,如图,
则CG∥DM,∠ACG=45°,∴AG=CG,
∵△AOC的面积为2,∴![]() ,解得:CG=1,
,解得:CG=1,
∴AG=1,∴OG=3,
∵C是OD的中点,CG∥DM,
∴DM=2CG=2,OM=2OG=6,
∴点D的坐标是(2,6);
(3)①证明:∵BE平分∠ABO,∴∠OBE=∠CBE,
又∵OB=CB,BE=BE,
∴△OBE≌△CBE(SAS),∴∠BCE=∠BOA=90°,即∠ACE=90°,
∵∠OAB =45°,∴∠AEC=45°,
∴ ∠AEC=∠CAE,∴CA=CE,
∴△ACE为等腰直角三角形;
②过点A作AH⊥OC交OC的延长线于点H,如图,
∵BC=BO,BE平分∠ABO,∴BF⊥OC,
∴∠AHC=∠CFE=90°,
∵∠CAH+∠ACH=90°,∠ECF+∠ACH=90°,
∴∠CAH=∠ECF,又∵AC=CE,
∴△ACH≌△CEF(AAS),∴EF=CH,
同理可证:△AOH≌△OBF(AAS),
∴OH=BF,
∴OC+EF=BF,即BF-EF=OC.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案