题目内容
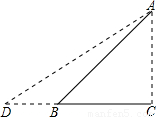
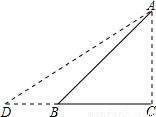
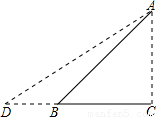
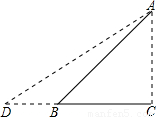
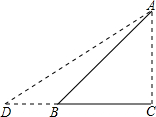 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).
解:Rt△ABC中,∠ABC=45°.
∴AC=AB•sin45°=12× =6
=6 米.
米.
∴BC=AC=6 米
米
Rt△ACD中,AD的坡比为1:1.5.
∴AC:CD=1:1.5.
∴CD=9 米,
米,
∴DB=DC-BC=3 米.
米.
分析:求DB的长,就要先求出CD和BC的长,也就是要先求出AC的长.直角三角形ACB中,有坡角的度数,有AB的长,易求得AC.
点评:两个直角三角形有公共的直角边,先求出公共边的解决此类题目的基本出发点.
∴AC=AB•sin45°=12×
 =6
=6 米.
米.∴BC=AC=6
 米
米Rt△ACD中,AD的坡比为1:1.5.
∴AC:CD=1:1.5.
∴CD=9
 米,
米,∴DB=DC-BC=3
 米.
米.分析:求DB的长,就要先求出CD和BC的长,也就是要先求出AC的长.直角三角形ACB中,有坡角的度数,有AB的长,易求得AC.
点评:两个直角三角形有公共的直角边,先求出公共边的解决此类题目的基本出发点.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
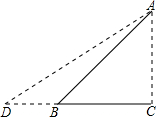 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45°,为了提高该堤的防洪能力,现把它改成坡比为1:1.5的斜坡AD.求DB的长(结果保留根号).