题目内容
 如图,已知:ABCD是正方形,E是CF上的一点,若DBEF是菱形,则∠EBC等于
如图,已知:ABCD是正方形,E是CF上的一点,若DBEF是菱形,则∠EBC等于
- A.15°
- B.22.5°
- C.30°
- D.25°
A
分析:过D作DG垂直于CF,垂足为G,由正方形的性质可得出正方形的四条边相等,且四个角为直角,三角形BCD为等腰直角三角形,可得出∠BDC与∠DBC都为45°,设正方形的边长为1,根据勾股定理求出BD的长为 ,即菱形的四条边为
,即菱形的四条边为 ,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为
,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为 ,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC-∠DBE求出度数即可.
,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC-∠DBE求出度数即可.
解答: 解:过D作DG⊥CF,垂足为G,如图所示:
解:过D作DG⊥CF,垂足为G,如图所示:
∵四边形ABCD为正方形,
∴∠CBD=∠CDB=45°,∠BCD=90°,
设正方形ABCD的边长为1,即AB=BC=CD=AD=1,
∴根据勾股定理得:BD= =
= ,
,
∵四边形BEFD为菱形,
∴BE=EF=DF=BD= ,
,
又BD∥EF,DG⊥FC,
∴BD⊥DG,即∠BDG=90°,
∴∠CDG=∠BDG-∠BDC=90°-45°=45°,又∠DGC=90°,
∴△DCG为等腰直角三角形,又DC=1,
∴DG=DCsin45°= ,又DF=
,又DF= ,
,
在Rt△DFG中,由DG= DF,
DF,
∴∠F=30°,
∴∠DBE=30°,
则∠EBC=∠DBC-∠DBE=45°-30°=15°.
故选A
点评:此题考查了正方形的性质,菱形的性质,等腰直角三角形的性质以及直角三角形的性质,根据题意作出辅助线DG是本题的突破点,熟练掌握图形的性质是解本题的关键.
分析:过D作DG垂直于CF,垂足为G,由正方形的性质可得出正方形的四条边相等,且四个角为直角,三角形BCD为等腰直角三角形,可得出∠BDC与∠DBC都为45°,设正方形的边长为1,根据勾股定理求出BD的长为
 ,即菱形的四条边为
,即菱形的四条边为 ,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为
,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为 ,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC-∠DBE求出度数即可.
,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC-∠DBE求出度数即可.解答:
 解:过D作DG⊥CF,垂足为G,如图所示:
解:过D作DG⊥CF,垂足为G,如图所示:∵四边形ABCD为正方形,
∴∠CBD=∠CDB=45°,∠BCD=90°,
设正方形ABCD的边长为1,即AB=BC=CD=AD=1,
∴根据勾股定理得:BD=
 =
= ,
,∵四边形BEFD为菱形,
∴BE=EF=DF=BD=
 ,
,又BD∥EF,DG⊥FC,
∴BD⊥DG,即∠BDG=90°,
∴∠CDG=∠BDG-∠BDC=90°-45°=45°,又∠DGC=90°,
∴△DCG为等腰直角三角形,又DC=1,
∴DG=DCsin45°=
 ,又DF=
,又DF= ,
,在Rt△DFG中,由DG=
 DF,
DF,∴∠F=30°,
∴∠DBE=30°,
则∠EBC=∠DBC-∠DBE=45°-30°=15°.
故选A
点评:此题考查了正方形的性质,菱形的性质,等腰直角三角形的性质以及直角三角形的性质,根据题意作出辅助线DG是本题的突破点,熟练掌握图形的性质是解本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
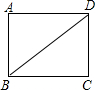 如图,已知矩形ABCD的对角线长为5,周长为14,AD>AB.
如图,已知矩形ABCD的对角线长为5,周长为14,AD>AB.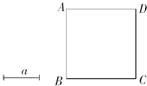 20、如图,已知正方形ABCD和线段a(a<AB).
20、如图,已知正方形ABCD和线段a(a<AB).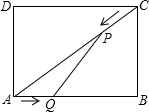 (2013•济南一模)如图,已知矩形ABCD中,AB=8cm,BC=6cm,如果点P由C出发沿CA方向向点A匀速运动,同时点Q由A出发沿AB方向向点B匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t.(单位:s).(0≤t≤4)解答下列问题:
(2013•济南一模)如图,已知矩形ABCD中,AB=8cm,BC=6cm,如果点P由C出发沿CA方向向点A匀速运动,同时点Q由A出发沿AB方向向点B匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t.(单位:s).(0≤t≤4)解答下列问题: (2011•资阳)如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.
(2011•资阳)如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F. (2013•下关区一模)如图,已知矩形ABCD中,A (3,2),B (3,-4),C (5,-4),点E是直线AB与x轴的交点,抛物线y=ax2+b x-3过点E,且顶点F的横坐标为1,点M是直线CD与x轴的交点.
(2013•下关区一模)如图,已知矩形ABCD中,A (3,2),B (3,-4),C (5,-4),点E是直线AB与x轴的交点,抛物线y=ax2+b x-3过点E,且顶点F的横坐标为1,点M是直线CD与x轴的交点.