��Ŀ����
 ��2013•�¹���һģ����ͼ����֪����ABCD�У�A ��3��2����B ��3��-4����C ��5��-4������E��ֱ��AB��x��Ľ��㣬������y=ax2+b x-3����E���Ҷ���F�ĺ�����Ϊ1����M��ֱ��CD��x��Ľ��㣮
��2013•�¹���һģ����ͼ����֪����ABCD�У�A ��3��2����B ��3��-4����C ��5��-4������E��ֱ��AB��x��Ľ��㣬������y=ax2+b x-3����E���Ҷ���F�ĺ�����Ϊ1����M��ֱ��CD��x��Ľ��㣮��1����a��b��ֵ��
��2������̽���ھ���ABCD���������ϣ��Ƿ���ڵ�P��ʹ�á�AFP�ǵ��������Σ�������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
��3�����������Ƿ���ڵ�Q�ڡ�EMC��ƽ�����ϣ�������ڣ������Q�����ꣻ��������ڣ���˵�����ɣ�
��������1�������E�����꣬����������y=ax2+bx-3����E���Ҷ���F�ĺ�����Ϊ1���г�����a��b�ķ����飬�ⷽ���鼴�����a��b��ֵ��
��2����������AFP�ǵ���������ʱ������������������ۣ�
��PA=PF���ַ������������i��P��AB���ϣ���ii��P��CD���ϣ����������ľ��빫ʽ�г����̣��ⷽ�̼��ɣ�
��AF=AP�����P���C�غϣ�
��FA=FP�����������ľ��빫ʽ�г����̣��ⷽ�̼��ɣ�
��3����Q�������Ϊ��x��x2-2x-3������x��5���ɵ�Q�ڡ�EMC��ƽ�����ϼ���Q��x��͵�ֱ��CD�ľ�����ȣ��г�����-��x2-2x-3��=5-x���ⷽ�����x��ֵ�����ɵõ���Q�����꣮
��2����������AFP�ǵ���������ʱ������������������ۣ�
��PA=PF���ַ������������i��P��AB���ϣ���ii��P��CD���ϣ����������ľ��빫ʽ�г����̣��ⷽ�̼��ɣ�
��AF=AP�����P���C�غϣ�
��FA=FP�����������ľ��빫ʽ�г����̣��ⷽ�̼��ɣ�
��3����Q�������Ϊ��x��x2-2x-3������x��5���ɵ�Q�ڡ�EMC��ƽ�����ϼ���Q��x��͵�ֱ��CD�ľ�����ȣ��г�����-��x2-2x-3��=5-x���ⷽ�����x��ֵ�����ɵõ���Q�����꣮
����⣺��1��A ��3��2����B ��3��-4������E��ֱ��AB��x��Ľ��㣬
��E��������3��0����
��������y=ax2+bx-3����E���Ҷ���F�ĺ�����Ϊ1��
��
�����
��
����a=1��b=-2��
 ��2���ھ���ABCD���������ϣ����ڵ�P��ʹ��������AFP�ǵ��������Σ��������£�
��2���ھ���ABCD���������ϣ����ڵ�P��ʹ��������AFP�ǵ��������Σ��������£�
�ٵ�PA=PFʱ����P���߶�AF�Ĵ�ֱƽ�����ϣ�
��i����P1���߶�AF�Ĵ�ֱƽ������AB�Ľ��㣬��BP1=x��
��P1A2=P1F2��
�ࣨ6-x��2=x2+22�����x=
��
���P��������3��-
����
��ii����P2���߶�AF�Ĵ�ֱƽ������CD�Ľ��㣬��CP2=y��
��P2A2=P2F2��
�ࣨ6-y��2+22=y2+42�����y=2��
 ���P��������5��-2����
���P��������5��-2����
�ڵ�AF=APʱ����P���C�غϣ�
��ʱ��P������Ϊ��5��-4����
�۵�FA=FPʱ����CP=m��
��FA2=FP2��
��62+22=m2+42�����m=2
��
���P��������5��2
-4����
���Ͽ�֪����P������Ϊ��3��-
����5��-2����5��-4����5��2
-4����
��3���������ϴ��ڵ�Q�ڡ�EMC��ƽ�����ϣ��������£�
�ɣ�1����y=x2-2x-3����Q�������Ϊ��x��x2-2x-3������x��5��
��Q�ڡ�EMC��ƽ�����ϼ���Q��x��͵�ֱ��CD�ľ�����ȣ�
����-��x2-2x-3��=5-x��
�����ã�x2-3x+2=0��
���x=1��2��
���Ե�Q������Ϊ��1��-4����2��-3����
��E��������3��0����
��������y=ax2+bx-3����E���Ҷ���F�ĺ�����Ϊ1��
��
|
|
����a=1��b=-2��
 ��2���ھ���ABCD���������ϣ����ڵ�P��ʹ��������AFP�ǵ��������Σ��������£�
��2���ھ���ABCD���������ϣ����ڵ�P��ʹ��������AFP�ǵ��������Σ��������£��ٵ�PA=PFʱ����P���߶�AF�Ĵ�ֱƽ�����ϣ�
��i����P1���߶�AF�Ĵ�ֱƽ������AB�Ľ��㣬��BP1=x��
��P1A2=P1F2��
�ࣨ6-x��2=x2+22�����x=
| 8 |
| 3 |
���P��������3��-
| 4 |
| 3 |
��ii����P2���߶�AF�Ĵ�ֱƽ������CD�Ľ��㣬��CP2=y��
��P2A2=P2F2��
�ࣨ6-y��2+22=y2+42�����y=2��
 ���P��������5��-2����
���P������Ϊ��5��-2�����ڵ�AF=APʱ����P���C�غϣ�
��ʱ��P������Ϊ��5��-4����
�۵�FA=FPʱ����CP=m��
��FA2=FP2��
��62+22=m2+42�����m=2
| 6 |
���P��������5��2
| 6 |
���Ͽ�֪����P������Ϊ��3��-
| 4 |
| 3 |
| 6 |
��3���������ϴ��ڵ�Q�ڡ�EMC��ƽ�����ϣ��������£�
�ɣ�1����y=x2-2x-3����Q�������Ϊ��x��x2-2x-3������x��5��
��Q�ڡ�EMC��ƽ�����ϼ���Q��x��͵�ֱ��CD�ľ�����ȣ�
����-��x2-2x-3��=5-x��
�����ã�x2-3x+2=0��
���x=1��2��
���Ե�Q������Ϊ��1��-4����2��-3����
�����������Ƕ��κ������ۺ����ͣ������漰����֪ʶ�������ô���ϵ�����������ߵĽ���ʽ�����������ε����ʣ������ľ��빫ʽ����ƽ���ߵ��ж����ۺ��Խ�ǿ���Ѷ����У��������ν�ϡ��������ۼ�����˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
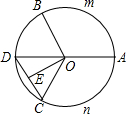 ��2013•�¹���һģ����ͼ��AD�ǡ�O��ֱ������AD=6����B��C�ڡ�O�ϣ�
��2013•�¹���һģ����ͼ��AD�ǡ�O��ֱ������AD=6����B��C�ڡ�O�ϣ�
