题目内容
已知抛物线的函数关系式:y=x2+2(a-1)x+a2-2a(其中x是自变量),(1)若点P(2,3)在此抛物线上,
①求a的值;
②若a>0,且一次函数y=kx+b的图象与此抛物线没有交点,请你写出一个符合条件的一次函数关系式(只需写一个,不要写过程);
(2)设此抛物线与轴交于点A(x1,0)、B(x2,0).若x1<
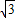 <x2,且抛物线的顶点在直线x=
<x2,且抛物线的顶点在直线x= 的右侧,求a的取值范围.
的右侧,求a的取值范围.
【答案】分析:(1)①将P点坐标代入抛物线的解析式中即可求出a的值.
②可根据①得出的a的值求出抛物线的解析式,然后根据抛物线的解析式即可写出符合条件的一次函数关系式.
(2)本题可从两方面考虑:
①根据x1<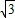 <x2,以及抛物线的开口向上可得出当x=
<x2,以及抛物线的开口向上可得出当x=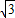 时,函数值必小于0,由此可得出一个a的取值范围.
时,函数值必小于0,由此可得出一个a的取值范围.
②由于抛物线的顶点在直线x= 的右侧,也就是说抛物线的对称轴在x=
的右侧,也就是说抛物线的对称轴在x= 的右侧,由此可得出另一个a的取值范围.结合两种情况即可求出a的取值范围.
的右侧,由此可得出另一个a的取值范围.结合两种情况即可求出a的取值范围.
解答:解:(1)①将P(2,3)代入y=x2+2(a-1)x+a2-2a
得a2+2a-3=0,(a+3)(a-1)=0
∴a=-3或a=1
②∵a>0,
∴由(1)知a=1,原函数化简为y=x2-1,
故与此抛物线无交点的直线可以是y=x-2.
(2)∵顶点在x= 右侧,即对称轴x=-
右侧,即对称轴x=-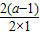 =1-a在
=1-a在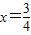 的右侧,
的右侧,
∴1-a>
∴a<
由于x1< <x2;
<x2;
∴抛物线在自变量取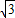 时,
时,
∵变量必小于0.
∴3+2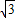 (a-1)+a2-2a<0;
(a-1)+a2-2a<0;
解得-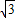 <a<2-
<a<2-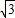
∵x=-(a-1)> ,即a<
,即a< ;
;
∴-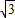 <a<
<a< .
.
点评:本题主要考查了二次函数的相关知识.
②可根据①得出的a的值求出抛物线的解析式,然后根据抛物线的解析式即可写出符合条件的一次函数关系式.
(2)本题可从两方面考虑:
①根据x1<
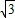 <x2,以及抛物线的开口向上可得出当x=
<x2,以及抛物线的开口向上可得出当x=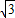 时,函数值必小于0,由此可得出一个a的取值范围.
时,函数值必小于0,由此可得出一个a的取值范围.②由于抛物线的顶点在直线x=
 的右侧,也就是说抛物线的对称轴在x=
的右侧,也就是说抛物线的对称轴在x= 的右侧,由此可得出另一个a的取值范围.结合两种情况即可求出a的取值范围.
的右侧,由此可得出另一个a的取值范围.结合两种情况即可求出a的取值范围.解答:解:(1)①将P(2,3)代入y=x2+2(a-1)x+a2-2a
得a2+2a-3=0,(a+3)(a-1)=0
∴a=-3或a=1
②∵a>0,
∴由(1)知a=1,原函数化简为y=x2-1,
故与此抛物线无交点的直线可以是y=x-2.
(2)∵顶点在x=
 右侧,即对称轴x=-
右侧,即对称轴x=-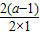 =1-a在
=1-a在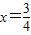 的右侧,
的右侧,∴1-a>

∴a<

由于x1<
 <x2;
<x2;∴抛物线在自变量取
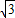 时,
时,∵变量必小于0.
∴3+2
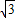 (a-1)+a2-2a<0;
(a-1)+a2-2a<0;解得-
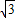 <a<2-
<a<2-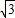
∵x=-(a-1)>
 ,即a<
,即a< ;
;∴-
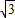 <a<
<a< .
.点评:本题主要考查了二次函数的相关知识.

练习册系列答案
相关题目
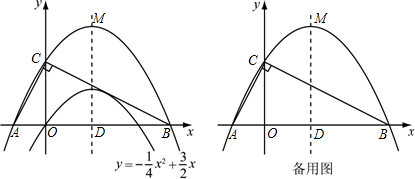
 且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,
且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切, (万元)的关系可用如图所示的抛物线和线段AB表示.其中A为抛物线的顶点.
(万元)的关系可用如图所示的抛物线和线段AB表示.其中A为抛物线的顶点.
 (2013•杭州一模)如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图;
(2013•杭州一模)如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图;