题目内容
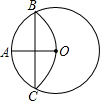 如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC=( )
如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC=( )A、3
| ||||
B、3
| ||||
C、
| ||||
D、
|
分析:先将圆补充完整,根据垂径定理和勾股定理利用特殊角的三角函数解答.
解答: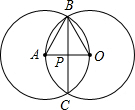 解:如图所示,AB=BO=AO,则△ABO为等边三角形,
解:如图所示,AB=BO=AO,则△ABO为等边三角形,
∴∠OBA=60°,
根据相交两圆的连心线垂直平分公共弦,则BP=PC=
BC,
∵△ABC为等边三角形,
∴BC是∠OBA的平分线,∠OBC=30°.
∴AP=
AB=
×3=
;
在Rt△ABP中,AB=3,AP=
,PB=
=
=
,
∴BC=2PB=2×
=3
;
故选B.
 解:如图所示,AB=BO=AO,则△ABO为等边三角形,
解:如图所示,AB=BO=AO,则△ABO为等边三角形,∴∠OBA=60°,
根据相交两圆的连心线垂直平分公共弦,则BP=PC=
| 1 |
| 2 |
∵△ABC为等边三角形,
∴BC是∠OBA的平分线,∠OBC=30°.
∴AP=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△ABP中,AB=3,AP=
| 3 |
| 2 |
| AB2-AP2 |
32-(
|
3
| ||
| 2 |
∴BC=2PB=2×
3
| ||
| 2 |
| 3 |
故选B.
点评:本题主要考查了垂径定理和勾股定理及相交两圆的连心线垂直平分公共弦的问题.

练习册系列答案
相关题目
 如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )
如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )| A、10 | B、8 | C、6 | D、4 |
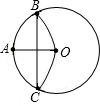 如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )A、6
| ||
B、6
| ||
C、3
| ||
D、3
|
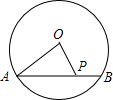 如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为
如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为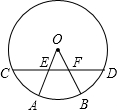 如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.
如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.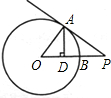 如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,
如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,