题目内容
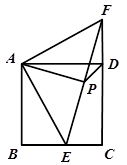
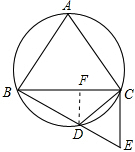
已知:如图,△ABC是⊙O的内接正三角形,点D是 的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.
的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.
(1)求证:△CDE是正三角形.
(2)问:△CDE经怎样的变换后能与△ABC成位似图形?请在图中直接画出△CDE变换后的对应三角形△CD'E',并求出△CD'E'与△ABC的位似比.

 的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.
的中点,连接BD并延长BD到点E,使BD=DE,连接CD和DE.(1)求证:△CDE是正三角形.
(2)问:△CDE经怎样的变换后能与△ABC成位似图形?请在图中直接画出△CDE变换后的对应三角形△CD'E',并求出△CD'E'与△ABC的位似比.

(1)见解析
(2)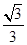 见解析
见解析
(2)
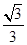 见解析
见解析解:(1)证明:∵△ABC是⊙O的内接正三角形,
∴∠BAC=60°,
∴∠CDE=60°,
∵点D是 的中点,
的中点,
∴BD=CD,
∵BD=DE,
∴CD=DE,
∴△CDE是正三角形;
(2)如图:当△CDE绕点C旋转∠ACD的度数时与△ABC成位似图形,
∵∠BDC=120°,BD=CD,
∴∠CBD=∠BCD=30°,
∵∠ACB=60°,
∴∠ACD=90°,
∴当△CDE绕点C旋转90°时与△ABC成位似图形,
作DF⊥BC于F点,
设DC=2x,
∵∠BCD=30°,
∴FC=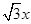 ,
,
∴BC=2FC=2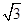 x,
x,
∴位似比=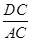 =
=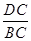 =
=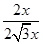 =
=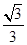 ,
,
∴位似比为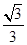 .
.

(1)利用圆内接四边形的性质可以求得∠BDC的度数,然后利用有一个角是60°的等腰三角形是等边三角形可以判定等边三角形;
(2)当CD与CA重合时,两三角形位似,所以当旋转∠ACD的度数的时候,两三角形位似,位似比等于CD与CA的比.∠B
∴∠BAC=60°,
∴∠CDE=60°,
∵点D是
 的中点,
的中点,∴BD=CD,
∵BD=DE,
∴CD=DE,
∴△CDE是正三角形;
(2)如图:当△CDE绕点C旋转∠ACD的度数时与△ABC成位似图形,
∵∠BDC=120°,BD=CD,
∴∠CBD=∠BCD=30°,
∵∠ACB=60°,
∴∠ACD=90°,
∴当△CDE绕点C旋转90°时与△ABC成位似图形,
作DF⊥BC于F点,
设DC=2x,
∵∠BCD=30°,
∴FC=
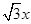 ,
,∴BC=2FC=2
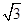 x,
x,∴位似比=
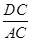 =
=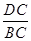 =
=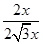 =
=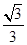 ,
,∴位似比为
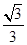 .
.

(1)利用圆内接四边形的性质可以求得∠BDC的度数,然后利用有一个角是60°的等腰三角形是等边三角形可以判定等边三角形;
(2)当CD与CA重合时,两三角形位似,所以当旋转∠ACD的度数的时候,两三角形位似,位似比等于CD与CA的比.∠B

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目


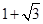 ,求△AEF的面积.
,求△AEF的面积.