题目内容
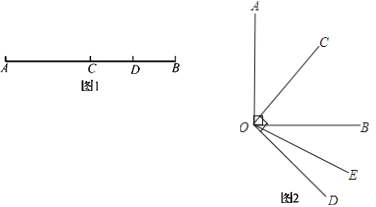
【题目】(1)如图1,已知点D是线段AC的中点,点B在线段DC上,且AB=4BC,若BD=6 cm,求AB的长;
(2)如图2,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,试求∠COE的度数.
【答案】(1)16 cm.(2)75°.
【解析】试题分析:(1)(1)根据AB=4BC,AB+BC=AC,可得AC=5BC,由线段中点的性质,可得AD=DC=![]() AC=
AC=![]() BC,再根据BD=DC-BC=6cm,可得关于BC的方程,根据解方程,可得BC的长,可得答案;
BC,再根据BD=DC-BC=6cm,可得关于BC的方程,根据解方程,可得BC的长,可得答案;
(2)根据角平分线的定义先求∠BOC的度数,即可求得∠BOD,再由∠BOD=3∠DOE,求得∠BOE.
解:(1)因为AB=4BC,AB+BC=AC,
所以AC=5BC.
因为点D是线段AC的中点,
所以AD=DC=![]() AC=
AC=![]() BC.
BC.
因为BD=DC-BC=6 cm,
所以![]() BC-BC=6 cm.
BC-BC=6 cm.
所以BC=4 cm.
所以AB=4BC=16 cm.
(2)因为∠AOB=90°,OC平分∠AOB,
所以∠BOC=![]() ∠AOB=45°.
∠AOB=45°.
因为∠BOD=∠COD-∠BOC=90°-45°=45°,∠BOD=3∠DOE,
所以∠DOE=15°.
所以∠COE=∠COD-∠DOE=90°-15°=75°.

练习册系列答案
相关题目
【题目】观察表格,结合其内容中所蕴含的规律和相关知识可知b=__________;
列举 | 猜想与发现 |
3,4,5 | 32=4+5 |
5,12,13 | 52=12+13 |
7,24,25 | 72=24+25 |
… | … |
17,b,c | 172=b+c |