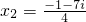题目内容
若用“i”表示虚数单位,且规定i2=-1,并用a+bi(a、b都是实数,且b≠0)表示一个任意的虚数,这样,我们把实数和虚数统称为复数,那么,在实数范围内无解的一元二次方程,在复数范围内就有解了.如方程x2-2x+2=0在复数范围内用公式法(用i2替换-1)解得其解为x1=1+i,x2=1-i,那么方程2x2+x+1=0在复数范围内的解为( )
分析:先运用求根公式法表示出x的值为x=
,再根据i2=-1就可以得到x=
,从而就可以求出结论.
-1+
| ||
| 4 |
-1+
| ||
| 4 |
解答:解:∵a=2,b=1,c=1,
∴b2-4ac=1-8=-7,
∴x=
.
∵i2=-1,
∴x=
,
∴x1=
,x2=
.
故选B.
∴b2-4ac=1-8=-7,
∴x=
-1+
| ||
| 4 |
∵i2=-1,
∴x=
-1+
| ||
| 4 |
∴x1=
-1+
| ||
| 4 |
-1-
| ||
| 4 |
故选B.
点评:本题考查了运用公式法求一元二次方程的解的运用,虚数的理解和认识,复数范围内求解的运用,解答时运用公式是关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
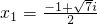 ,
,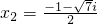
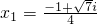 ,
,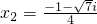
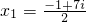 ,
,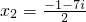
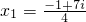 ,
,