题目内容
下图是行列间隔都为1个单位的点阵:①你能计算点阵中多边形的面积吗?请将答案直接填入图中横线上.
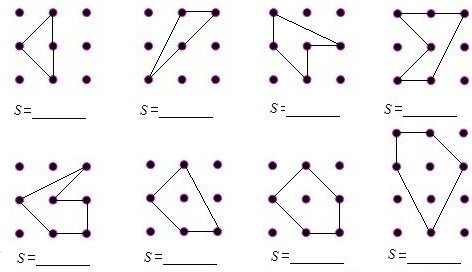
②若用a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积,你能用含a和b的代数式表示S=
③请你利用②中的公式来求a=4,b=20时,多边形的面积S.
分析:(1)分别计算出各个多边形的面积,通过归纳分析可以发现:多边形的面积等于多边形内部的点数加上
与多边形边界上的点数的乘积然后减去1.
(2)按照(1)中总结的规律,将表示多边形内部的点数a,表示多边形边界上的点数b,表示多边形的面积S代入即可得到答案.
(3)将a=4,b=20代入s=a+
b-1中,即可直接球的多边形的面积.
| 1 |
| 2 |
(2)按照(1)中总结的规律,将表示多边形内部的点数a,表示多边形边界上的点数b,表示多边形的面积S代入即可得到答案.
(3)将a=4,b=20代入s=a+
| 1 |
| 2 |
解答:解:(1)因为点阵中行列间隔都为1个单位,
所以,第一个多边形的面积为1=0+
×4-1;
第二个多边形的面积为1=0+
×4-1;
第三个多边形的面积为
=0+
×5-1;
第四个多边形的面积为2=0+
×6-1;
第五个多边形的面积为2=0+
×6-1;
第六个多边形的面积为2=1+
×4-1;
第七个多边形的面积为
=1+
×5-1;
第三个多边形的面积为
=2+
×5-1;
通过计算,并对上述结果进行归纳总结可以发现:
等号左边的数为多边形的面积,等号右边的第一个数是多边形内部的点数,第二个和第四个数都是常数,
第三个数是多边形边界上的点数.
所以说多边形的面积等于多边形内部的点数加上
与多边形边界上的点数的乘积然后减去1.
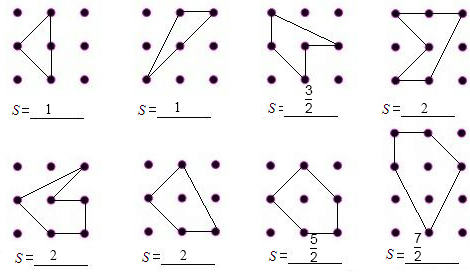
(2)若用a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积,
按照(1)中总结的规律,则有:s=a+
b-1.
(3)当a=4,b=20时,a+
b-1=4+10-1=13•
所以,第一个多边形的面积为1=0+
| 1 |
| 2 |
第二个多边形的面积为1=0+
| 1 |
| 2 |
第三个多边形的面积为
| 3 |
| 2 |
| 1 |
| 2 |
第四个多边形的面积为2=0+
| 1 |
| 2 |
第五个多边形的面积为2=0+
| 1 |
| 2 |
第六个多边形的面积为2=1+
| 1 |
| 2 |
第七个多边形的面积为
| 5 |
| 2 |
| 1 |
| 2 |
第三个多边形的面积为
| 7 |
| 2 |
| 1 |
| 2 |
通过计算,并对上述结果进行归纳总结可以发现:
等号左边的数为多边形的面积,等号右边的第一个数是多边形内部的点数,第二个和第四个数都是常数,
第三个数是多边形边界上的点数.
所以说多边形的面积等于多边形内部的点数加上
| 1 |
| 2 |

(2)若用a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积,
按照(1)中总结的规律,则有:s=a+
| 1 |
| 2 |
(3)当a=4,b=20时,a+
| 1 |
| 2 |
点评:此题主要考查学生对图形变化类这个知识点的理解和掌握,解答此类题目的关键是根据题目中给出的图形,数值等条件,认真分析,找到规律.此类题目难度一般偏大,属于难题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目

