题目内容
【题目】如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数 ![]() 的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为 .
的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为 . 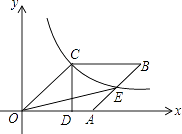
【答案】2 ![]() ﹣2
﹣2
【解析】解:过点E作EF⊥x轴,交x轴于点F, 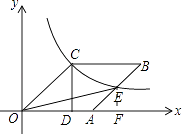
∵OD=2,即C横坐标为2,
∴把x=2代入反比例解析式得:y=2,即C(2,2),
∴CD=OD=2,即△OCD为等腰直角三角形,
∵四边形ABCO为菱形,
∴OC∥AB,OA=OC=2 ![]() ,
,
∴∠EAF=45°,
设EF=AF=x,则有OF=OA+AF=2 ![]() +x,
+x,
∴E(2 ![]() +x,x),
+x,x),
把E坐标代入反比例解析式得:x(2 ![]() +x)=4,
+x)=4,
解得:x=﹣ ![]() +
+ ![]() (负值舍去),
(负值舍去),
则△OAE面积S= ![]() OAEF=
OAEF= ![]() ×2
×2 ![]() ×(﹣
×(﹣ ![]() +
+ ![]() )=2
)=2 ![]() 2.
2.
所以答案是:2 ![]() ﹣2
﹣2
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半).

练习册系列答案
相关题目



