题目内容
【题目】在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2 . 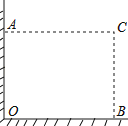
(1)求这地面矩形的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
【答案】
(1)
解:设这地面矩形的长是xm,则依题意得:
x(20﹣x)=96,
解得x1=12,x2=8(舍去),
答:这地面矩形的长是12米
(2)
解:规格为0.80×0.80所需的费用:96×(0.80×0.80)×55=8250(元).
规格为1.00×1.00所需的费用:96×(1.00×1.00)×80=7680(元).
因为8250<7680,
所以采用规格为1.00×1.00所需的费用较少
【解析】(1)根据题意表示出长方形的长,进而利用长×宽=面积,求出即可;(2)分别计算出每一规格的地板砖所需的费用,然后比较即可.此题主要考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
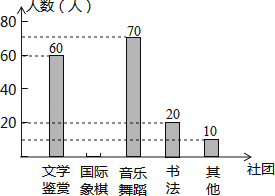
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.