题目内容
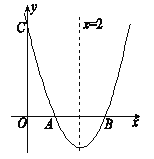
【题目】已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).

(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式和∠ABC的度数;
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)45°;(3)P(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)直接将A,C点坐标代入抛物线解析式求出即可;
(2)首先求出B点坐标,进而利用待定系数法求出直线BC的解析式,进而利用CO,BO的长求出∠ABC的度数;
(3)利用∠ACB=∠PAB,结合相似三角形的判定与性质得出BP的长,进而得出P点坐标.
解:(1)将点A的坐标(﹣1,0),点C的坐标(0,﹣3)代入抛物线解析式得:
![]() ,
,
解得:![]() ,
,
故抛物线解析式为:y=x2﹣2x﹣3;
(2)由(1)得:0=x2﹣2x﹣3,
解得:x1=﹣1,x2=3,故B点坐标为:(3,0),
设直线BC的解析式为:y=kx+d,
则![]() ,
,
解得:![]() ,
,
故直线BC的解析式为:y=x﹣3,
∵B(3,0),C(0,﹣3),
∴BO=OC=3,
∴∠ABC=45°;
(3)过点P作PD⊥x轴于点D,
∵∠ACB=∠PAB,∠ABC=∠PBA,
∴△ABP∽△CBA,
∴![]() =
=![]() ,
,
∵BO=OC=3,
∴BC=3![]() ,
,
∵A(﹣1,0),B(3,0),
∴AB=4,
∴![]() =
=![]() ,
,
解得:BP=![]() ,
,
由题意可得:PD∥OC,
∴DB=DP=![]() ,
,
∴OD=3﹣![]() =
=![]() ,
,
则P(![]() ,﹣
,﹣![]() ).
).


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目