题目内容
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-![]() x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
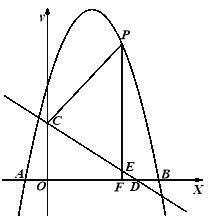
(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
【答案】(1)、y=-![]() +4x+5;(2)、m=2或m=
+4x+5;(2)、m=2或m=![]() ;(3)、
;(3)、![]() ,
,![]() (4,5),
(4,5),![]() .
.
【解析】
试题分析:(1)、利用待定系数法进行求解;(2)、首先设出点P、点E和点F的坐标,求出PE的长度,然后根据点E在点F的上方和下方两种情况分别进行计算;(3)、根据△CME和△COD相似来进行求解.
试题解析:(1)、将A、B两点的坐标代入得:![]() 解得:
解得:![]()
∴抛物线的解析式为:y=-![]() +4x+5
+4x+5
、设点P的坐标为(m,-![]() +4m+5),则E(m,-
+4m+5),则E(m,-![]() m+3),F(m,0)
m+3),F(m,0)
∵点P在x轴上方,要使PE=5EF,点P应在y轴右侧 ∴0<m<5
PE=-![]() +4m+5-(-
+4m+5-(-![]() m+3)=-
m+3)=-![]() +
+![]() m+2
m+2
①当点E在点F上方时,EF=-![]() m+3 ∵PE=5EF ∴-
m+3 ∵PE=5EF ∴-![]() +
+![]() m+2=5(-
m+2=5(-![]() m+3)
m+3)
解得:![]() =2,
=2,![]() (舍去)
(舍去)
②当点E在点F下方时,EF=![]() m-3 ∵PE=5EF ∴-
m-3 ∵PE=5EF ∴-![]() +
+![]() m+2=5(
m+2=5(![]() m-3)
m-3)
解得:![]() ,
,(舍去)
(3)、点P的坐标为![]() ,
,![]() (4,5),
(4,5),![]()

练习册系列答案
相关题目