题目内容
12.已知直角三角形两条边的长分别为3cm、4cm,那么斜边上的高是$\frac{3\sqrt{7}}{4}$或$\frac{12}{5}$cm.分析 直角三角形中斜边为最长边,无法确定边长为4cm的边是否为斜边,所以要讨论(1)边长为4cm的边为斜边;(2)边长为4cm的边为直角边;由三角形面积即可得出结果.
解答 解:设斜边上的高为h,分两种情况:
(1)当边长为4cm的边为斜边时,
该直角三角形中斜边长为4cm,一条直角边长为3cm,
另一条直角边长=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$(cm);
斜边上的高h=$\frac{3×\sqrt{7}}{4}$=$\frac{3\sqrt{7}}{4}$;
(2)当边长为4cm的边为直角边时,
则根据勾股定理得斜边长为$\sqrt{{3}^{2}+{4}^{2}}$=5(cm),
斜边上的高h=$\frac{3×4}{5}$=$\frac{12}{5}$(cm);
故该直角三角形斜边上的高为$\frac{3\sqrt{7}}{4}$cm或$\frac{12}{5}$cm,
故答案 为$\frac{3\sqrt{7}}{4}$或$\frac{12}{5}$.
点评 本题考查了勾股定理在直角三角形中的运用,考查了分类讨论思想,本题中运用分类讨论思想讨论边长为4cm的边是直角边还是斜边是解题的关键.

练习册系列答案
相关题目
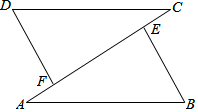 如图DF⊥AC于点F,BE⊥AC于点E,AB=CD,AF=CE.求证:BE=DF.
如图DF⊥AC于点F,BE⊥AC于点E,AB=CD,AF=CE.求证:BE=DF. 已知两个有理数a,b在数轴上的位置如图所示:
已知两个有理数a,b在数轴上的位置如图所示: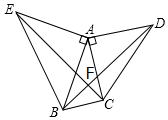 如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上.
如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上.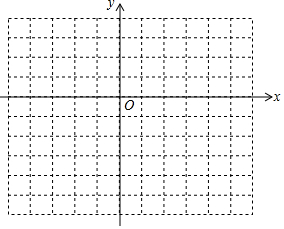 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上,且A(1,-4),B(5,-4),C(4,-1)
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点在格点上,且A(1,-4),B(5,-4),C(4,-1)