题目内容
17.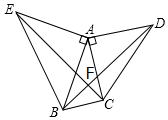 如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上.
如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上.
分析 由△ABD和△ACE都是等腰直角三角形得出AB=AE,AD=AC,∠BAE=∠CAD=90°,再进一步得出∠EAC=∠BAD证得△ABD≌△AEC,过点A分别作AM⊥BD,AN⊥EC,垂足为点M,N.根据三角形的面积公式求出AN=AM,根据角平分线性质求出即可.
解答 解:∵△ABE和△ACD都是等腰直角三角形,
∴AB=AD,AE=AC,
又∵∠BAE=∠CAD=90°,
∴∠BAE+∠BAC=∠CAD+∠BAC,
即:∠EAC=∠BAD,
在△ABD和△AEC中,
$\left\{\begin{array}{l}{AB=AE}\\{∠EAC=∠BAD}\\{AD=AC}\end{array}\right.$,
∴△ABD≌△AEC( SAS)
∴BD=EC,
如图,过点A分别作AM⊥BD,AN⊥EC,垂足为点M,N.
∵△ABD≌△AEC,
∴S△ABD=S△AEC,
∴$\frac{1}{2}$BD•AM=$\frac{1}{2}$CE•AN,
∴AM=AN,
∴点A在∠DFE的平分线上,
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图弓形中,AB=30$\sqrt{3}$,弓高h为15,求:
如图弓形中,AB=30$\sqrt{3}$,弓高h为15,求: 如图,平面直角坐标系中,矩形ABCO的边OA,OC分别在坐标轴上,OA=2,OC=1,以点A为顶点的抛物线经过点C
如图,平面直角坐标系中,矩形ABCO的边OA,OC分别在坐标轴上,OA=2,OC=1,以点A为顶点的抛物线经过点C