Question

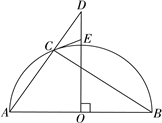
【题目】如图，AB是半圆的直径，过圆心O作AB的垂线，与弦AC的延长线交于点D，点E在OD上．

（1）求证：CE是半圆的切线；

（2）若CD=10，，求半圆的半径．

Answer 1

【答案】（1）见解析；(2)

【解析】分析: （1）连接CO，由且OC=OB,得,利用同角的余角相等判断出∠BCO+∠BCE=90°，即可得出结论；
（2）设AC=2x，由根据题目条件用x分别表示出OA、AD、AB，通过证明△AOD∽△ACB，列出等式即可.

详解：（1）证明：如图，连接CO.

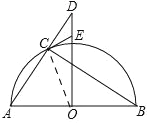
∵AB是半圆的直径，

∴∠ACB=90°.

∴∠DCB=180°-∠ACB=90°.

∴∠DCE+∠BCE=90°.

∵OC=OB,

∴∠OCB=∠B.

∵，

∴∠OCB=∠DCE.

∴∠OCE=∠DCB=90°.

∴OC⊥CE.

∵OC是半径，

∴CE是半圆的切线.

（2）解：设AC=2x，

∵在Rt△ACB中，,

∴BC=3x.

∴.

∵OD⊥AB,

∴∠AOD=∠ACB=90°.

∵∠A=∠A，

∴△AOD∽△ACB.

∴.

∵，AD=2x+10,

∴.

解得 x=8.

∴.

则半圆的半径为.