题目内容
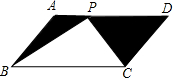
如图，分别延长?ABCD的边BA、DC到点E、H，使得AE=AB，CH=CD，连接EH，分别交AD、BC于点F、G．
求证：△AEF≌△CHG．
求证：△AEF≌△CHG．
证明：在?ABCD中，AB∥CD，AB=CD，
∴∠E=∠H，∠EAF=∠D，
∵四边形ABCD是平行四边形，
∴∠BAD=∠BCD，
∴∠EAF=∠HCG，
∵AE=AB，CH=CD，
∴AE=CH，
在△AEF与△CHG中，
∴△AEF≌△CHG（ASA）．
∴∠E=∠H，∠EAF=∠D，
∵四边形ABCD是平行四边形，
∴∠BAD=∠BCD，
∴∠EAF=∠HCG，
∵AE=AB，CH=CD，
∴AE=CH，
在△AEF与△CHG中，
|
∴△AEF≌△CHG（ASA）．
练习册系列答案
相关题目
的取值范围；
