Question

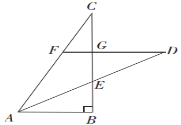
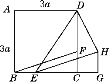
【题目】如图所示，正方形ABCD的边长为3a，两动点E，F分别从顶点B，C同时开始以相同速度沿边BC，CD运动，与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF，B，E，C，G在一条直线上．

(1)若BE＝a，求DH的长．

(2)当E点在BC边上的什么位置时，△DHE的面积取得最小值？并求该三角形面积的最小值．

Answer 1

【答案】（1）DH＝a；（2）△DHE的面积取得最小值，最小值是a2.

【解析】

仔细审题，根据已知点E与点F的移动，得到BE=CF，由已知△BCF≌△EGH，利用全等三角形的性质得到HG＝FC，∠G＝∠BCF，连接FH，根据前面所得的条件，不难得到四边形EBFH是平行四边形，△DFH是直角三角形，再利用勾股定理第一问就可求解；对于（2），要得到△DHE面积的最小值，设BE=x，根据y=S△CDE+S梯形CDHE-S△EGH=×3a×(3a－x)＋ (3a＋x)x－×3a×x，结合二次函数求最值的方法即可完成解答.

(1)如图，连接FH，∵△EGH≌△BCF，

∴HG＝FC，∠G＝∠BCF，

∴HG∥FC，

∴四边形FCGH是平行四边形，

∴FH=CG，

∴∠DFH＝∠DCG＝90°.

由题意可知，CF＝BE＝a.在Rt△DFH中，DF＝3a－a＝2a，FH＝a，

∴DH＝a.

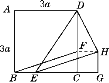
(2)设BE＝x，△DHE的面积为y.

依题意，得y＝S△CDE＋S梯形CDHG－S△EGH＝×3a×(3a－x)＋ (3a＋x)x－×3a×x，

∴y＝x2－ax＋a2，即y＝＋a2.

∴当x＝a，即E是BC的中点时，y取得最小值，即△DHE的面积取得最小值，最小值是a2.