题目内容
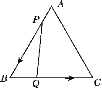
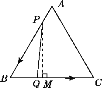
【题目】如图,△ABC是边长为3 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1 cm/s,当点P运动到B时,P,Q两点停止运动,设P点运动时间为t(s).
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y关于t的函数表达式,当t取何值时,四边形APQC的面积最小?并求出最小面积.
【答案】(1)当t为1或2时,△PBQ是直角三角形;(2)当t为![]() 时,四边形APQC的面积最小,最小面积为
时,四边形APQC的面积最小,最小面积为![]() cm2.
cm2.
【解析】
(1)分情况进行讨论:①∠BPQ=90°;②∠BQP=90°;在直角三角形中利用30°角所对直角边等于斜边一半求解即可;
(2)用△ABC的面积-△PBQ的面积表示出四边形APQC的面积,即可得出y,t的函数关系式,再将函数关系式转化为顶点式,即可求出最小值.
(1)由题意可知,∠B=60°,BP=(3-t)cm,BQ=tcm.若△PBQ是直角三角形,则∠BPQ=30°或∠BQP=30°,于是BQ=![]() BP或BP=
BP或BP=![]() BQ,即t=
BQ,即t=![]() (3-t)或3-t=
(3-t)或3-t=![]() t.解得t=1或t=2,即当t为1或2时,△PBQ是直角三角形.
t.解得t=1或t=2,即当t为1或2时,△PBQ是直角三角形.
(2)如图,过点P作PM⊥BC于点M,
则易知BM=![]() BP=
BP=![]() (3-t)cm.
(3-t)cm.
∴PM=![]() =
=![]() (3-t)cm.
(3-t)cm.
∴S四边形APQC=S△ABC-S△PBQ=![]() ×3×
×3×![]() -
-![]() t·
t·![]() (3-t)=
(3-t)=![]() t2-
t2-![]() t+
t+![]() ,即y=
,即y=![]() t2-
t2-![]() t+
t+![]() ,易知0<t<3.
,易知0<t<3.
于是y=![]() (t-
(t-![]() )2+
)2+![]()
∴当t=![]() 时,y取得最小值,为
时,y取得最小值,为![]()
即当t为![]() 时,四边形APQC的面积最小,最小面积为
时,四边形APQC的面积最小,最小面积为![]() cm2.
cm2.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目