题目内容
【题目】如图，等腰直角三角形
分别沿着某条直线对称得到图形
．若上述对称关系保持不变，平移
，使得四个图形能够围成一个不重叠且无缝隙的正方形，此时点
的坐标和正方形的边长为（ ）
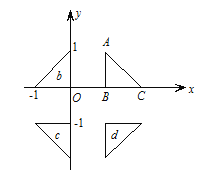
A. 
B. 
C. 
D. 
【答案】D
【解析】分析：根据在轴对称图形中，对称轴两侧的对应点到对称轴的距离相等，结合等腰直角三角形的性质，以及正方形的性质可知，△ABC移动时，其它三个对称三角形保持关系不变的随之移动，对称中心也就是最后的四个图形的相交公共点，其在坐标中的位置的横、纵坐标的长度等于右上角的三角形相应边边长的一半，然后根据点在第四象限写出即可．由正方形的面积等于4个三角形的面积和，即可得出正方形的边长．
详解：根据图形可知，AB=1，BC=1，∴移动后，点B的横坐标与纵坐标的长度都是
，又点B移动后位于第四象限，∴此时点B的坐标为（，﹣）．
∵正方形的面积=4××1×1=2，∴边长为：
．
故选D．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
