题目内容
在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10.点E在下底边BC上,点F在腰AB上.(1)若EF平分等腰梯形ABCD的周长,设BE长为x,试用含x的代数式表示△BEF的面积;
(2)是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在,求出此时BE的长;若不存在,请说明理由;
(3)是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1:2的两部分?若存在,求出此时BE的长;若不存在,请说明理由.

【答案】分析:(1)先作AK⊥BC于K,FG⊥BC于G,根据等腰梯形的性质,可得BK= (BC-AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=
(BC-AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=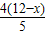 ,利用面积公式可得S△BEF=-
,利用面积公式可得S△BEF=- x2+
x2+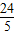 x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);
x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);
(2)根据题意,结合(1)中面积的表达式,可以得到 S梯形ABCD=-
S梯形ABCD=- x2+
x2+ x,即14=-
x,即14=- x2+
x2+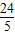 x,解得,x1=7,x2=5(不合题意,舍去);
x,解得,x1=7,x2=5(不合题意,舍去);
(3)仍然按照(1)和(2)的步骤和方法去做就可以了,注意不是分成相等的两份,而是1:2就可以了,得到关于x的一元二次方程,先求出根的判别式△,由于△<0,故不存在实数根.
解答: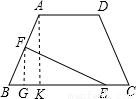 解:(1)由已知条件得:
解:(1)由已知条件得:
梯形周长为24,高4,面积为28.
过点F作FG⊥BC于G
∴BK= (BC-AD)=
(BC-AD)= ×(10-4)=3,
×(10-4)=3,
∴AK=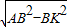 =4,
=4,
∵EF平分等腰梯形ABCD的周长,设BE长为x,
∴BF=12-x,
过点A作AK⊥BC于K
∴△BFG∽△BAK,
∴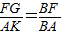 ,
,
即: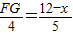 ,
,
则可得:FG=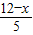 ×4
×4
∴S△BEF= BE•FG=-
BE•FG=- x2+
x2+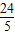 x(7≤x≤10);(3分)
x(7≤x≤10);(3分)
(2)存在(1分)
由(1)得:- x2+
x2+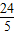 x=14,
x=14,
x2-12x+35=0,
(x-7)(x-5)=0,
解得x1=7,x2=5(不合题意舍去)
∴存在线段EF将等腰梯形ABCD的周长与面积同时平分,此时BE=7;
(3)不存在(1分)
假设存在,第一种情况:显然是:S△BEF:SAFECD=1:2,(BE+BF):(AF+AD+DC+CE)=1:2(1分),
梯形ABCD周长的三分之一为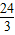 =8,面积的三分之一为
=8,面积的三分之一为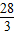 .因为BE=X,
.因为BE=X,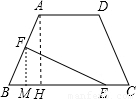
所以BF=(8-X)
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴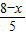 =
=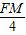 ,
,
∴FM=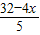 ,
,
∴△BEF的面积=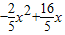 ,
,
当 梯形ABCD的面积=
梯形ABCD的面积=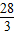 时,
时,
∴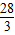 =
=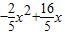 ,
,
整理方程得:-3x2+24x-70=0,
△=576-840<0
∴不存在这样的实数x.
即不存在线段EF将等腰梯形ABCD的周长和面积.
同时分成1:2的两部分.(2分)
第二种情况:显然是:S△BEF:SAFECD=2:1,(BE+BF):(AF+AD+DC+CE)=2:1(1分),
梯形ABCD周长的三分之一为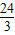 =8,面积的三分之一为
=8,面积的三分之一为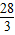 .因为BE=x,
.因为BE=x,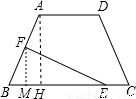
所以BF=(8-x)
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴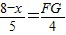 ,
,
∴FM=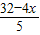 ,
,
∴△BEF的面积=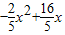 ,
,
当 梯形ABCD的面积=
梯形ABCD的面积=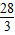 时,
时,
∴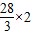 =
=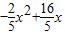 ,
,
整理方程得:3x2-24x+140=0,
△<0
∴不存在这样的实数x.
即不存在线段EF将等腰梯形ABCD的周长和面积.
同时分成1:2的两部分.
点评:本题利用了等腰梯形的性质、垂直于同一直线的两直线平行,勾股定理,三角形、梯形面积公式,解一元二次方程,以及一元二次方程根的判别式等知识.
 (BC-AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=
(BC-AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=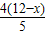 ,利用面积公式可得S△BEF=-
,利用面积公式可得S△BEF=- x2+
x2+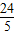 x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);
x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);(2)根据题意,结合(1)中面积的表达式,可以得到
 S梯形ABCD=-
S梯形ABCD=- x2+
x2+ x,即14=-
x,即14=- x2+
x2+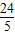 x,解得,x1=7,x2=5(不合题意,舍去);
x,解得,x1=7,x2=5(不合题意,舍去);(3)仍然按照(1)和(2)的步骤和方法去做就可以了,注意不是分成相等的两份,而是1:2就可以了,得到关于x的一元二次方程,先求出根的判别式△,由于△<0,故不存在实数根.
解答:
 解:(1)由已知条件得:
解:(1)由已知条件得:梯形周长为24,高4,面积为28.
过点F作FG⊥BC于G
∴BK=
 (BC-AD)=
(BC-AD)= ×(10-4)=3,
×(10-4)=3,∴AK=
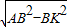 =4,
=4,∵EF平分等腰梯形ABCD的周长,设BE长为x,
∴BF=12-x,
过点A作AK⊥BC于K
∴△BFG∽△BAK,
∴
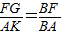 ,
,即:
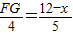 ,
,则可得:FG=
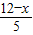 ×4
×4∴S△BEF=
 BE•FG=-
BE•FG=- x2+
x2+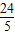 x(7≤x≤10);(3分)
x(7≤x≤10);(3分)(2)存在(1分)
由(1)得:-
 x2+
x2+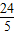 x=14,
x=14,x2-12x+35=0,
(x-7)(x-5)=0,
解得x1=7,x2=5(不合题意舍去)
∴存在线段EF将等腰梯形ABCD的周长与面积同时平分,此时BE=7;
(3)不存在(1分)
假设存在,第一种情况:显然是:S△BEF:SAFECD=1:2,(BE+BF):(AF+AD+DC+CE)=1:2(1分),
梯形ABCD周长的三分之一为
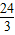 =8,面积的三分之一为
=8,面积的三分之一为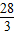 .因为BE=X,
.因为BE=X,
所以BF=(8-X)
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴
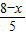 =
=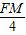 ,
,∴FM=
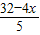 ,
,∴△BEF的面积=
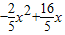 ,
,当
 梯形ABCD的面积=
梯形ABCD的面积=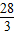 时,
时,∴
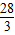 =
=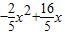 ,
,整理方程得:-3x2+24x-70=0,
△=576-840<0
∴不存在这样的实数x.
即不存在线段EF将等腰梯形ABCD的周长和面积.
同时分成1:2的两部分.(2分)
第二种情况:显然是:S△BEF:SAFECD=2:1,(BE+BF):(AF+AD+DC+CE)=2:1(1分),
梯形ABCD周长的三分之一为
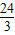 =8,面积的三分之一为
=8,面积的三分之一为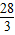 .因为BE=x,
.因为BE=x,
所以BF=(8-x)
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴
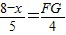 ,
,∴FM=
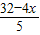 ,
,∴△BEF的面积=
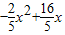 ,
,当
 梯形ABCD的面积=
梯形ABCD的面积=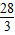 时,
时,∴
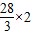 =
=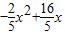 ,
,整理方程得:3x2-24x+140=0,
△<0
∴不存在这样的实数x.
即不存在线段EF将等腰梯形ABCD的周长和面积.
同时分成1:2的两部分.
点评:本题利用了等腰梯形的性质、垂直于同一直线的两直线平行,勾股定理,三角形、梯形面积公式,解一元二次方程,以及一元二次方程根的判别式等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC. 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.