题目内容
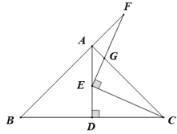
【题目】如图,Rt△ABC 中,AB=AC,∠BAC=90°,AD 是 BC 边上的高,E 是 AD 上的一点。连接 EC,过点 E 作 EF⊥EC 交射线 BA 于点 F,EF、AC 交于点 G。若 DE=3,△EGC 与△AFG 面积的差是 2,则 BD=_____.
【答案】5
【解析】
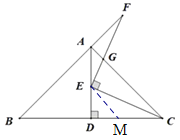
在DC上取点M,使DM=DE,连接EM,通过证明FAEEMC,根据△EGC 与△AFG 面积的差是 2,推出△EAC 与△EMC 面积的差是 2,然后设MC=x,则AE=x,AD=x+3,利用面积差即可求出x,即可求出BD.
解:在DC上取点M,使DM=DE,连接EM
∵Rt△ABC,AB=AC,AD ⊥ BC
∴BD=CD=AD,∠EAF=135°
同理∠EMC=135°
∴AE=CM
∠AEF+∠CED=∠ECM+∠CED=90°
∴∠AEF=∠ECM
∴FAEEMC
∵S△EGC -S△AFG=2
∴S△EAC -S△FAE=2
∴S△EAC -S△EMC=2
设MC=x,则AE=x,AD=x+3
∵S△EAC=![]() ,S△MEC=
,S△MEC=![]()
∴![]() -
-![]() =2
=2
解得x=2(x>0,负值舍去),
∴AD=2+3=5
∴BD=AD=5
故答案为:5.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目