题目内容
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
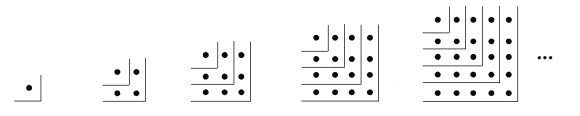
(1)在④和⑤后面的横线上分别写出相应的等式:
①1=12;②1+3=22;③1+3+5=32;④_____________;⑤_____________;….
(2)通过猜想写出与第n个点阵图相对应的等式.
【答案】(1) 1+3+5+7=42; 1+3+5+7+9=52;(2)1+3+5+…+(2n-1)=n2.
【解析】
根据图示和数据可知规律是:等式左边是连续的奇数和,等式右边是等式左边的首数与末数的平均数的平方,据此进行解答即可.
(1)由图①知黑点个数为1个,
由图②知在图①的基础上增加3个,
由图③知在图②基础上增加5个,
则可推知图④应为在图③基础上增加7个即有1+3+5+7=42,
图⑤应为1+3+5+7+9=52,
故答案为:④1+3+5+7=42;⑤1+3+5+7+9=52;
(2)由(1)中推理可知第n个图形黑点个数为1+3+5+…+(2n-1)=n2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车收费标准有两种类型,如下表:
里程 | 甲类收费(元) | 乙类收费(元) |
3千米以下(包含3千米) | 7.00 | 6.00 |
3千米以上,每增加1千米 | 1.60 | 1.40 |
(1)设出租车行驶的里程为x千米(![]() 且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
(2)小华身上仅有11元,他乘出租车到科技馆车费够不够请说明理由.



