题目内容
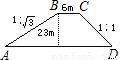
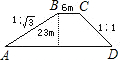 一拦水坝的横断面是梯形ABCD(如图),坝顶宽6m,坝高23m,斜坡AB的坡度i=1
一拦水坝的横断面是梯形ABCD(如图),坝顶宽6m,坝高23m,斜坡AB的坡度i=1| 3 |
| 3 |
分析:(1)已知了斜坡AB的坡度,即可得到坡角a的正切值,由此可求得a的度数;
(2)已知了梯形的高,可过B、C作下底的垂线,设垂足为E、F;分别在Rt△ABE、Rt△CFD中,根据铅直高度和各自的坡度求得AE、FD的长,进而由AD=AE+BC+DF求出坝底宽AD的长.
(2)已知了梯形的高,可过B、C作下底的垂线,设垂足为E、F;分别在Rt△ABE、Rt△CFD中,根据铅直高度和各自的坡度求得AE、FD的长,进而由AD=AE+BC+DF求出坝底宽AD的长.
解答: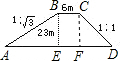 解:作BE⊥AD,CF⊥AD,E、F分别为垂足;(1分)
解:作BE⊥AD,CF⊥AD,E、F分别为垂足;(1分)
∵斜坡AB的坡度i=1
,
∴tanα=
∴α=30°(2分)
在Rt△AEB中,AE=
=23
(3分)
在Rt△CFD中,
∵
=1,
∴FD=CF=23;
∴AD=AE+EF+FD=23
+6+23≈68.8;
答:斜坡AB的坡角α为30°,坝底宽AD约是68.8m.(4分)
 解:作BE⊥AD,CF⊥AD,E、F分别为垂足;(1分)
解:作BE⊥AD,CF⊥AD,E、F分别为垂足;(1分)∵斜坡AB的坡度i=1
| 3 |
∴tanα=
| ||
| 3 |
∴α=30°(2分)
在Rt△AEB中,AE=
| BE |
| tanα |
| 3 |
在Rt△CFD中,
∵
| CF |
| FD |
∴FD=CF=23;
∴AD=AE+EF+FD=23
| 3 |
答:斜坡AB的坡角α为30°,坝底宽AD约是68.8m.(4分)
点评:应用问题尽管题型千变万化,但关键是设法化归为解直角三角形问题,必要时应添加辅助线,构造出直角三角形.

练习册系列答案
相关题目
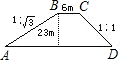 一拦水坝的横断面是梯形ABCD(如图),坝顶宽6m,坝高23m,斜坡AB的坡度i=1
一拦水坝的横断面是梯形ABCD(如图),坝顶宽6m,坝高23m,斜坡AB的坡度i=1 ,斜坡CD的坡度i′=1:1,求斜坡AB的坡角α及坝底宽AD(精确到0.1m,
,斜坡CD的坡度i′=1:1,求斜坡AB的坡角α及坝底宽AD(精确到0.1m,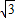 ,斜坡CD的坡度i′=1:1,求斜坡AB的坡角α及坝底宽AD(精确到0.1m,
,斜坡CD的坡度i′=1:1,求斜坡AB的坡角α及坝底宽AD(精确到0.1m,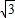 =1.732)
=1.732)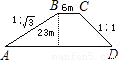
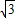 ,斜坡CD的坡度i′=1:1,求斜坡AB的坡角α及坝底宽AD(精确到0.1m,
,斜坡CD的坡度i′=1:1,求斜坡AB的坡角α及坝底宽AD(精确到0.1m,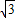 =1.732)
=1.732)