题目内容
【题目】已知点A、B在数轴上分别表示a,b.请认真观察数轴及表格再解答问题:
![]()

(1)表格中的m=_____,n=________
(2)若A、B两点间的距离记为d,则d与a、b间的等量关系为__________
(3)结合上述结论,并利用数轴解答下列问题
①满足到表示数4和-6的点的距离之和等于16的数为
②若点C表示的数为x,求![]() 的最小值.(本页可作为草稿纸使用)
的最小值.(本页可作为草稿纸使用)
【答案】(1)2,12;(2)![]() ;(3)①7或-9,②7
;(3)①7或-9,②7
【解析】
(1)根据数轴和表即可得出结论;
(2)根据数轴上任意两点之间的距离公式即可写出;
(3)①设这个数为x,由 (2)的结论,列出含绝对值的方程,然后对x进行分类讨论,去绝对值并解方程即可;
②根据(2)的结论,对x进行分类讨论,然后分别求出![]() 的取值范围,即可求出
的取值范围,即可求出![]() 的最小值.
的最小值.
解:(1)由数轴和表可知:当a=﹣6,b=﹣4时,AB两点之间的距离:m=2,
当a=2,b=﹣10时,AB两点之间的距离:n=12
(2)根据数轴上任意两点之间的距离可得:![]()
(3)①设这个数为x,由 (2)的结论可知:![]()
当![]() 时,
时,![]()
解得:![]() ;
;
当![]() 时,
时,![]()
此方程无解;
当![]() 时,
时,![]()
解得:![]()
综上所述:这个数为7或-9
②由(2)的结论可知:
![]() 表示x到﹣2的距离,
表示x到﹣2的距离,![]() 表示x到5的距离
表示x到5的距离
当![]() 时,x到5的距离大于7个单位长度,所以
时,x到5的距离大于7个单位长度,所以![]() ;
;
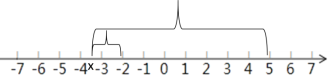
当![]() 时,x到﹣2的距离加上x到5的距离等于7个单位长度,所以
时,x到﹣2的距离加上x到5的距离等于7个单位长度,所以![]() ;
;
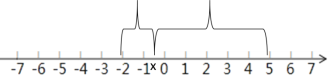
当![]() 时,x到﹣2的距离大于7个单位长度,所以
时,x到﹣2的距离大于7个单位长度,所以![]()

所以![]() ,即
,即![]() 的最小值为7.
的最小值为7.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目