题目内容
如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD=DC:AB,④S△AOD=S△BOC,其中始终正确的有( )个.

A.1
B.2
C.3
D.4
【答案】分析:根据已知及相似三角形的判定方法对各个选项进行分析从而得到最后答案.
解答:解:∵AB∥CD,
∴△AOB∽△COD(①正确),
∴S△DOC:S△AOD= =
=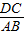 (③正确),
(③正确),
∵△ABD与△ABC等高同底,
∴S△ABD=S△ABC,
∵S△ABD-S△AOB=S△ABC-S△AOB,
∴S△AOD=S△BOC(④正确),
∵梯形ABCD是任意梯形,
∴△AOD和△ACB不可能相似,
故②错误,
∴共有3个正确的.
故选C.
点评:此题考查了相似三角形的判定和性质:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.相似三角形的对应边成比例,对应角相等.相似三角形的对应高、对应中线,对应角平分线的比等于相似比,相似三角形的周长比等于相似比,相似三角形的面积比等于相似比的平方.
解答:解:∵AB∥CD,
∴△AOB∽△COD(①正确),
∴S△DOC:S△AOD=
 =
=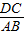 (③正确),
(③正确),∵△ABD与△ABC等高同底,
∴S△ABD=S△ABC,
∵S△ABD-S△AOB=S△ABC-S△AOB,
∴S△AOD=S△BOC(④正确),
∵梯形ABCD是任意梯形,
∴△AOD和△ACB不可能相似,
故②错误,
∴共有3个正确的.
故选C.
点评:此题考查了相似三角形的判定和性质:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.相似三角形的对应边成比例,对应角相等.相似三角形的对应高、对应中线,对应角平分线的比等于相似比,相似三角形的周长比等于相似比,相似三角形的面积比等于相似比的平方.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
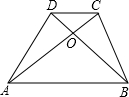 如图,梯形ABCD的对角线交于点O,有以下四个结论:
如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD=DC:AB,④S△AOD=S△BOC,其中始终正确的有( )个.
| A、1 | B、2 | C、3 | D、4 |
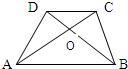
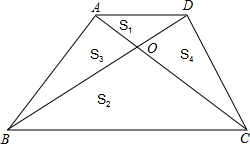 如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )
如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
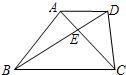 14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
 16、如图,梯形ABCD的对角线交于点O,有以下三个结论:
16、如图,梯形ABCD的对角线交于点O,有以下三个结论: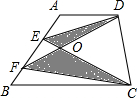 如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为
如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为