题目内容
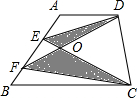 如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为
如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为分析:已知AE=BF,可设梯形的高为H,E到AD的距离为m.则可根据梯形性质和三角形面积求解.
解答:解:设梯形的高为H,E到AD的距离为m.
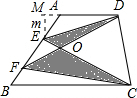
则:S△ADE+S△BCF=
m ①
S△ADF+S△BCE=
•( H-m) ②
①+②=
•H,正好是梯形的面积,
∴S△ADE+S△BCF+S△EOF=S△COD,
所以S△EOD+S△COF=34-11×2=12.
故答案为:12.

则:S△ADE+S△BCF=
| AD+BC |
| 2 |
S△ADF+S△BCE=
| AD+BC |
| 2 |
①+②=
| AD+BC |
| 2 |
∴S△ADE+S△BCF+S△EOF=S△COD,
所以S△EOD+S△COF=34-11×2=12.
故答案为:12.
点评:本题考查了梯形和三角形的面积,难度较大,做题关键是记住等底等高的三角形面积相等.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
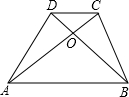 如图,梯形ABCD的对角线交于点O,有以下四个结论:
如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD=DC:AB,④S△AOD=S△BOC,其中始终正确的有( )个.
| A、1 | B、2 | C、3 | D、4 |
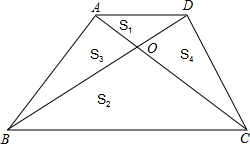 如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )
如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
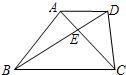 14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
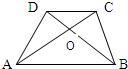 16、如图,梯形ABCD的对角线交于点O,有以下三个结论:
16、如图,梯形ABCD的对角线交于点O,有以下三个结论: