题目内容
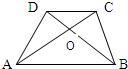 16、如图,梯形ABCD的对角线交于点O,有以下三个结论:
16、如图,梯形ABCD的对角线交于点O,有以下三个结论:(1)△AOB∽△COD;(2)△AOD∽△ACB;(3)S△AOD=S△BOC.
其中正确的结论有( )
分析:题中已知了四边形ABCD是梯形,那么可根据AB∥CD和相似三角形的判定方法进行求解.
解答:解:(1)正确,根据CD∥AB,即可得出两三角形相似;
(2)不正确,无法证得两三角形的对应角相等;
(3)正确,根据等高三角形的面积比等于底边比,可得:S△AOD:S△COD=AO:OC,
同理可得出:S△BOC:S△COD=BO:OD;
由于△COD∽△AOB,因此AO:OC=BO:OD,即S△AOD:S△COD=S△BOC:S△COD,
即S△AOD=S△BOC,从而得到其面积相等.
所以正确的共有两个.
故选:C
(2)不正确,无法证得两三角形的对应角相等;
(3)正确,根据等高三角形的面积比等于底边比,可得:S△AOD:S△COD=AO:OC,
同理可得出:S△BOC:S△COD=BO:OD;
由于△COD∽△AOB,因此AO:OC=BO:OD,即S△AOD:S△COD=S△BOC:S△COD,
即S△AOD=S△BOC,从而得到其面积相等.
所以正确的共有两个.
故选:C
点评:此题主要考查学生对相似三角形的判定方法的掌握情况.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
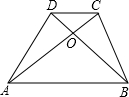 如图,梯形ABCD的对角线交于点O,有以下四个结论:
如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD,②△AOD∽△ACB,③S△DOC:S△AOD=DC:AB,④S△AOD=S△BOC,其中始终正确的有( )个.
| A、1 | B、2 | C、3 | D、4 |
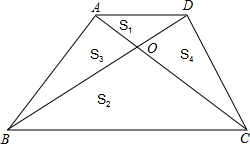 如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )
如图,梯形ABCD的对角线AC、BD相交于点O,△ADO的面积记作S1,△BCO的面积记作S2,△ABO的面积记作S3,△CDO的面积记作S4,则下列关系正确是( )| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
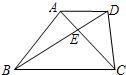 14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
14、如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
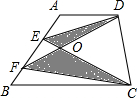 如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为
如图,梯形ABCD的面积为34cm2,AE=BF,CE与DF相交于O,△OCD的面积为11cm2,则阴影部分的面积为