题目内容
（2004•天津）已知x2+y2=25，x+y=7，且x＞y，则x-y的值等于 ．
【答案】分析：运用完全平方公式先求出x-y的平方，结合已知条件求出2xy的值，从而求出（x-y）2的值，最后根据x、y的大小，开平方求解．
解答：解：∵x2+y2=25，x+y=7
∴（x+y）2=x2+2xy+y2=49，
解得2xy=24，
∴（x-y）2=x2-2xy+y2=25-24=1，
又因为x＞y
∴x-y=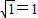
．
点评：本题主要考查完全平方公式的变形，熟记公式结构是解题的关键，需要注意，因为x＞y，所以最后结果只有一个．
解答：解：∵x2+y2=25，x+y=7
∴（x+y）2=x2+2xy+y2=49，
解得2xy=24，
∴（x-y）2=x2-2xy+y2=25-24=1，
又因为x＞y
∴x-y=
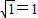．点评：本题主要考查完全平方公式的变形，熟记公式结构是解题的关键，需要注意，因为x＞y，所以最后结果只有一个．
练习册系列答案
相关题目
（2004•天津）已知一次函数y1=2x，二次函数y2=x2+1．
（Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
（Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
（Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．
（Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
| x | -3 | -2 | -1 | 1 | 2 | 3 | |
| y1=2x | |||||||
| y2=x2+1 |
（Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．
（m≠-1）的图象在第一象限内的交点为P（x，3）．
（m≠-1）的图象在第一象限内的交点为P（x，3）．