题目内容
（2004•天津）已知一次函数y=x+m与反比例函数y=
（m≠-1）的图象在第一象限内的交点为P（x，3）．（1）求x的值；
（2）求一次函数和反比例函数的解析式．
【答案】分析：（1）已知一次函数y=x+m与反比例函数y=
（m≠-1）的图象在第一象限内的交点为P（x，3），把P点的坐标代入两个解析式就可以解决；
（2）在（1）的基础上，进一步求得m的值．
解答：解：（1）∵点P（x，3）在一次函数y=x+m的图象上．
∴3=x+m，即m=3-x．
又点P（x，3）在反比例函数y=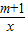
的图象上，
∴3=
，即m=3x-1．
∴3-x=3x-1，
解得x=1；
（2）由（1），得
m=3-x=3-1=2，
∴一次函数的解析式为y=x+2，反比例函数的解析式为y=
．
点评：本题考查了函数的图象与解析式的关系：点在图象上，就一定满足函数的解析式．同时还考查了利用待定系数法求函数解析式的方法．
（m≠-1）的图象在第一象限内的交点为P（x，3），把P点的坐标代入两个解析式就可以解决；（2）在（1）的基础上，进一步求得m的值．
解答：解：（1）∵点P（x，3）在一次函数y=x+m的图象上．
∴3=x+m，即m=3-x．
又点P（x，3）在反比例函数y=
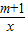的图象上，∴3=
，即m=3x-1．∴3-x=3x-1，
解得x=1；
（2）由（1），得
m=3-x=3-1=2，
∴一次函数的解析式为y=x+2，反比例函数的解析式为y=
．点评：本题考查了函数的图象与解析式的关系：点在图象上，就一定满足函数的解析式．同时还考查了利用待定系数法求函数解析式的方法．
练习册系列答案
名校课堂系列答案
相关题目
（2004•天津）已知一次函数y1=2x，二次函数y2=x2+1．
（Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
（Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
（Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．
（Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
| x | -3 | -2 | -1 | 1 | 2 | 3 | |
| y1=2x | |||||||
| y2=x2+1 |
（Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．
（m≠-1）的图象在第一象限内的交点为P（x，3）．