题目内容
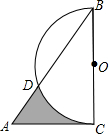 如图,以Rt△ABC的直角边BC为直径画半圆,交斜边AB于D,若AC=
如图,以Rt△ABC的直角边BC为直径画半圆,交斜边AB于D,若AC=| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
分析:连接CD、OD.
阴影部分的面积即为三角形ACD的面积加上三角形OCD的面积减去扇形OCD的面积.
根据切割线定理求得AD的长,进而求得BC、AC的长和扇形的圆心角的度数.
阴影部分的面积即为三角形ACD的面积加上三角形OCD的面积减去扇形OCD的面积.
根据切割线定理求得AD的长,进而求得BC、AC的长和扇形的圆心角的度数.
解答: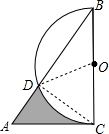 解:连接CD、OD.
解:连接CD、OD.
∵AC⊥BC,
∴AC是⊙O的切线,
∴AC2=AD•AB.
设AD=x,则AB=x+
.
则(
)2=x(x+
),
解之,得x1=
,x2=-
(舍去).
∴AD=
,AB=
,
∠B=3O°,BC=2,CD=1.
S阴影=S△ACD+S△OCD-S扇形OCD
=
+
-
π=
×1.73-
×3.14
=0.72-0.52=0.2.
 解:连接CD、OD.
解:连接CD、OD.∵AC⊥BC,
∴AC是⊙O的切线,
∴AC2=AD•AB.
设AD=x,则AB=x+
| 3 |
则(
| 2 |
| 3 |
| 3 |
| 3 |
解之,得x1=
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
∴AD=
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
∠B=3O°,BC=2,CD=1.
S阴影=S△ACD+S△OCD-S扇形OCD
=
| 1 |
| 6 |
| 3 |
| 1 |
| 4 |
| 3 |
| 1 |
| 6 |
| 5 |
| 12 |
| 1 |
| 6 |
=0.72-0.52=0.2.
点评:能够把不规则图形的面积转化为规则图形的面积.
熟练运用切割线定理、扇形的面积公式和三角形的面积公式.
熟练运用切割线定理、扇形的面积公式和三角形的面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD.
23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD.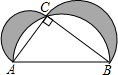 如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是
如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是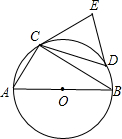 已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.
已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.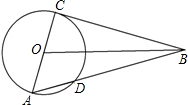 如图,以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D,若劣弧CD=120°,则
如图,以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D,若劣弧CD=120°,则 (2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
(2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.