Question

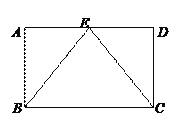
【题目】（1）如图，在四边形ABCD是矩形，点E是AD的中点，求证：EB=EC．

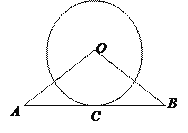
（2）如图，AB与相切于C，，⊙O的半径为6，AB＝16，求OA的长.

Answer 1

【答案】（1）见解析；（2）10.

【解析】

(1)利用SAS证明△ABE≌△DCE，根据全等三角形性质即可得；

（2）连接OC，则有OC⊥AB，再根据等腰三角形的判定与性质可得AC长，在直角三角形OAC中，利用勾股定理即可求得OA长.

（1）∵四边形ABCD是矩形，

∴∠A=∠D=90° ，AB=DC，

又∵AE=DE，

∴△ABE≌△DCE（SAS），

∴EB=EC；

（2）如图，连接OC，

∵AB与相切于C，

∴OC⊥AB，

∵∠A=∠B，

∴OA=OB，

∴AC=BC=AB=×16=8，

在Rt△OAC中，OA2=OC2+AC2，

∴OA==10.