ЬтФПФкШн
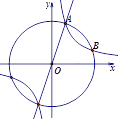
ЁОЬтФПЁПвбжЊ:ШчЭМ1ЃЌЯпЖЮABЁЂCDЯрНЛгкЕуOЃЌСЌНгADЁЂCBЃЌШчЭМ2ЃЌдкЭМ1ЕФЬѕМўЯТЃЌЁЯDABКЭЁЯBCDЕФЦНЗжЯпAPКЭCPЯрНЛгкЕуPЃЌВЂЧвгыCDЁЂABЗжБ№ЯрНЛгкMЁЂNЃЌЪдНтД№ЯТСаЮЪЬтЃК
(1)дкЭМ1жаЃЌЧыжБНгаДГіЁЯAЁЂЁЯBЁЂЁЯCЁЂЁЯDжЎМфЕФЪ§СПЙиЯЕ:_____________________ЃЛ
(2)дкЭМ2жаЃЌШєЁЯD=40ЁуЃЌЁЯB=30ЁуЃЌЪдЧѓЁЯPЕФЖШЪ§(аДГіНтД№Й§ГЬ)ЃЛ
(3)ШчЙћЭМ2жаЃЌЁЯDКЭЁЯBЮЊШЮвтНЧЃЌЦфЫћЬѕМўВЛБфЃЌЪдаДГіЁЯPгыЁЯDЁЂЁЯBжЎМфЕФЪ§СПЙиЯЕ(жБНгаДГіНсТлМДПЩ).

ЁОД№АИЁПЃЈ1ЃЉЁЯA+ЁЯD=ЁЯB+ЁЯCЃЛЃЈ2ЃЉ35ЁуЃЛЃЈ3ЃЉ2ЁЯP=ЁЯB+ЁЯD
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнШ§НЧаЮЕФФкНЧКЭЕШгк180ЁуЃЌвзЕУЁЯA+ЁЯD=ЁЯB+ЁЯCЃЛ
ЃЈ2ЃЉзаЯИЙлВьЭМ2ЃЌЕУЕНСНИіЙиЯЕЪНЁЯ1+ЁЯD=ЁЯ3+ЁЯPЃЌЁЯ2+ЁЯP=ЁЯ4+ЁЯBЃЌдйгЩНЧЦНЗжЯпЕФаджЪЕУЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4ЃЌСНЪНЯрМѕЃЌМДПЩЕУНсТлЃЎ
ЃЈ3ЃЉВЮееЃЈ2ЃЉЕФНтЬтЫМТЗ.
НтЃКЃЈ1ЃЉЁЯA+ЁЯD=ЁЯB+ЁЯCЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕУЃЌЁЯ1+ЁЯD=ЁЯ3+ЁЯPЃЌЁЯ2+ЁЯP=ЁЯ4+ЁЯBЃЌ
ЁрЁЯ1-ЁЯ3=ЁЯP-ЁЯDЃЌЁЯ2-ЁЯ4=ЁЯB-ЁЯPЃЌ
гжЁпAPЁЂCPЗжБ№ЦНЗжЁЯDABКЭЁЯBCDЃЌ
ЁрЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4ЃЌ
ЁрЁЯP-ЁЯD=ЁЯB-ЁЯPЃЌ
МД2ЁЯP=ЁЯB+ЁЯDЃЌ
ЁрЁЯP=ЃЈ40Ёу+30ЁуЃЉЁТ2=35ЁуЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕФНтЬтВНжшПЩжЊЃЌЁЯPгыЁЯDЁЂЁЯBжЎМфЕФЪ§СПЙиЯЕЮЊЃК2ЁЯP=ЁЯB+ЁЯDЃЎ

 аТЫМЮЌМйЦкзївЕЪюМйМЊСжДѓбЇГіАцЩчЯЕСаД№АИ
аТЫМЮЌМйЦкзївЕЪюМйМЊСжДѓбЇГіАцЩчЯЕСаД№АИЁОЬтФПЁПФГЪЏЛЏввЯЉГЇФГГЕМфЩњВњМзЁЂввСНжжЫмСЯЕФЯрЙиаХЯЂШчЯТБэЃЌЧыФуНтД№ЯТСаЮЪЬтЃК
ГіГЇМл | ГЩБОМл | ХХЮлДІРэЗб | |
МзжжЫмСЯ | 2100ЃЈдЊ/ЖжЃЉ | 800ЃЈдЊ/ЖжЃЉ | 200ЃЈдЊ/ЖжЃЉ |
ввжжЫмСЯ | 2400ЃЈдЊ/ЖжЃЉ | 1100ЃЈдЊ/ЖжЃЉ | 100ЃЈдЊ/ЖжЃЉ СэУПдТЛЙашжЇИЖЩшБИЙмРэЁЂЮЌЛЄЗб20000дЊ |
ЃЈ1ЃЉЩшИУГЕМфУПдТЩњВњМзЁЂввСНжжЫмСЯИїxЖжЃЌРћШѓЗжБ№ЮЊy1дЊКЭy2дЊЃЌЗжБ№ЧѓГіy1КЭy2гыxЕФКЏЪ§ЙиЯЕЪН(зЂЃКРћШѓ=змЪеШы-змжЇГі)ЃЛ
ЃЈ2ЃЉвбжЊИУГЕМфУПдТЩњВњМзЁЂввСНжжЫмСЯОљВЛГЌЙ§400ЖжЃЌШєФГдТвЊЩњВњМзЁЂввСНжжЫмСЯЙВ700ЖжЃЌЧѓИУдТЩњВњМзЁЂввЫмСЯИїЖрЩйЖжЪБЃЌЛёЕУЕФзмРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП