题目内容
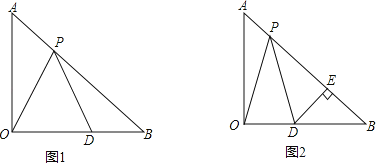
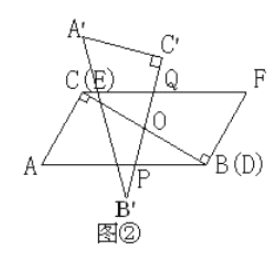
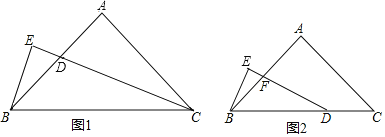
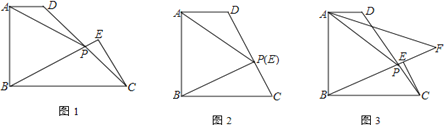
【题目】如图1,在直角梯形ABCD中,AB⊥BC,AD∥BC,点P为DC上一点,且AP=AB,过点C作CE⊥BP交直线BP于E.
(1) 若![]() ,求证:
,求证:![]() ;
;
(2) 若AB=BC.
① 如图2,当点P与E重合时,求![]() 的值;
的值;
② 如图3,设∠DAP的平分线AF交直线BP于F,当CE=1,![]() 时,直接写出线段AF的长.
时,直接写出线段AF的长.
【答案】(1)证明见解析;(2)①![]() ;②3.
;②3.
【解析】
(1) 过点A作AF⊥BP于F,根据等腰三角形的性质得到BF=BP,易证Rt△ABF∽Rt△BCE,根据相似三角形的性质得到![]() ,即可证明BP=
,即可证明BP=![]() CE.
CE.
(2) ①延长BP、AD交于点F,过点A作AG⊥BP于G,证明△ABG≌△BCP,根据全等三角形的性质得BG=CP,设BG=1,则PG=PC=1,BC=AB=![]() ,在Rt△ABF中,由射影定理知,AB2=BG·BF=5,即可求出BF=5,PF=5-1-1=3,即可求出
,在Rt△ABF中,由射影定理知,AB2=BG·BF=5,即可求出BF=5,PF=5-1-1=3,即可求出![]() 的值;
的值;
② 延长BF、AD交于点G,过点A作AH⊥BE于H,证明△ABH≌△BCE,根据全等三角形的性质得BG=CP,设BH=BP=CE=1,又![]() ,得到PG=
,得到PG=![]() ,BG=
,BG=![]() ,根据射影定理得到AB2=BH·BG ,即可求出AB=
,根据射影定理得到AB2=BH·BG ,即可求出AB=![]() ,根据勾股定理得到
,根据勾股定理得到
![]() ,根据等腰直角三角形的性质得到
,根据等腰直角三角形的性质得到![]() .
.
解:(1) 过点A作AF⊥BP于F
∵AB=AP
∴BF=BP,
∵Rt△ABF∽Rt△BCE
∴![]()
∴BP=![]() CE.
CE.

(2) ①延长BP、AD交于点F,过点A作AG⊥BP于G

∵AB=BC
∴△ABG≌△BCP(AAS)
∴BG=CP
设BG=1,则PG=PC=1
∴BC=AB=![]()
在Rt△ABF中,由射影定理知,AB2=BG·BF=5
∴BF=5,PF=5-1-1=3
∴![]()
② 延长BF、AD交于点G,过点A作AH⊥BE于H
∵AB=BC
∴△ABH≌△BCE(AAS)
设BH=BP=CE=1
∵![]()
∴PG=![]() ,BG=
,BG=![]()
∵AB2=BH·BG
∴AB=![]()
∴![]()
∵AF平分∠PAD,AH平分∠BAP
∴∠FAH=∠BAD=45°
∴△AFH为等腰直角三角形
∴![]()

 阅读快车系列答案
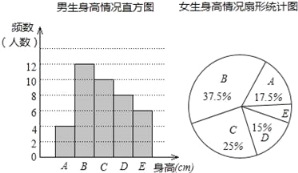
阅读快车系列答案【题目】为了了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<160 |
B | 160≤x<165 |
C | 165≤x<170 |
D | 170≤x<175 |
E | x≥175 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生600人,女生480人,请估计身高在165≤x<175之间的学生约有多少人?