题目内容
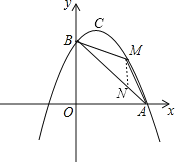
【题目】如图，以直线x＝1为对称轴的抛物线y＝ax2＋bx＋c(a，b，c为常数)经过A(4，0)和B(0，4)两点，其顶点为C.
(1)求该抛物线的表达式及其顶点C的坐标；
(2)若点M是抛物线上的一个动点，且位于第一象限内．
①设△ABM的面积为S，试求S的最大值；
②若S为整数，则这样的M点有 个．
【答案】(1)抛物线表达式为y＝－
x2＋x＋4,顶点坐标为(1， 
);
(2) ①S△ABM的最大值为4; ②3.
【解析】试题分析： 
先利用抛物线的对称性确定抛物线与
轴的另一个交点坐标，再设交点式
然后把
点坐标代入求出
即可得到抛物线的解析式，再把解析式配成顶点式可得
的坐标；
①过
点作
轴交
于
点，如图，利用待定系数法求出直线
的解析式，则可设
则
于是用
可表示出
，再利用
得到
与
的二次函数，然后根据二次函数的性质求解；
②在
的取值范围内找出整数使对应的函数值为整数即可确定点
的位置．
试题解析： 
∵抛物线的对称轴为直线
抛物线与
轴的一个交点为
∴抛物线与
轴的另一个交点为
设抛物线的解析式为
把
代入得
解得
∴抛物线的解析式为
即
∴抛物线的顶点
的坐标为
(2)①过
点作
轴交
于
点，如图，
设
的解析式为
把
代入得
解得
∴直线
的解析式为
设
则
∴当
时， 
有最大值，最大值为
；
②
∴当
时， 
为整数，
即这样的
点有
个.
故答案为
.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】在不透明的袋子中有四张标着数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏．小明画出树状图如图所示：
小华列出表格如下：
1 | 2 | 3 | 4 | |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
（1）根据树形图分析，小明的游戏规则是，随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片；根据表格分析，小华的游戏规则是，随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片。
（2）根据小华的游戏规则，表格中①表示的有序数对为 。
（3）规定两次抽到的数字之和为奇数的获胜，谁获胜的可能性大？为什么？
