Question

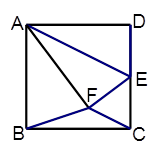
如图，已知正方形ABCD的边长为4，点E为边DC的中点，连结AE,,将△ADE沿着AE翻折，使点D落在正方形内的点F处，连结BF、CF,则S△BFC的面积为            .

Answer 1

.

试题分析：延长AF交BC于点H，过F作FG⊥BC于G，连接CH.可证FH=CH，由勾股定理可求FH=CH=1，根据相似三角形可求BG=，CG=.从而S_△BFC=S_{正方形ABCD}-S_△ABF-S_△CEF-2S_△ADE
试题解析：延长AF交BC于点H，过F作FG⊥BC于G，连接CH.如图：

由折叠的性质知：AD=AF=4，DE=FE=2．
在△EFH与△ECH中，∠EFH=∠ECH=90°，EH＝EH，EC＝EF，
∴△EFH≌△ECH（HL），
∴HF=CH．
设FH=x，则CH=x，AH=4+x，BH=4-x，
在Rt△ABH中，由勾股定理可得：AB²+BH²=AH²，
即4²+（4-x）²=（4+x）²，解得x=1.
∴BH=4-1=3．AH=4+1=5.
又△ABH∽△FGH
∴
即：
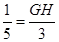
∴GH=，BG=3-=
∴S_△BFC=S_{正方形ABCD}-S_△ABF-S_△CEF-2S_△ADE=4×4-×4×-×2×-2××4×2=.
考点: 1.翻折变换（折叠问题）；2.正方形的性质．