题目内容
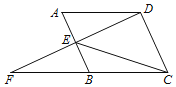
【题目】如图1,在![]() 中,
中,![]() 是BC上的一点,以AD为边作
是BC上的一点,以AD为边作![]() ,使
,使![]() .
.
(1)直接用含![]() 的式子表示
的式子表示![]() 的度数是_______________;
的度数是_______________;
(2)以![]() 为边作平行四边形
为边作平行四边形![]() ;
;
①如图2,若点F恰好落在DE上,试判断线段BD与线段CD的长度是否相等,并说明理由.
②如图3,若点F落在是DE上,且![]() ,求线段CF的长(直接写出结果,不说明理由).
,求线段CF的长(直接写出结果,不说明理由).

【答案】(1)![]() ;(2)①相等,见解析,②
;(2)①相等,见解析,②![]()
【解析】
(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
(1)∵在△ABC中,AB=AC,∠ABC=α,
∴∠BAC=180°2α,
∵∠DAE+∠BAC=180°,
∴∠DAE=2α,
∵AE=AD,
∴∠ADE=90°α;
故答案为:90°α;
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°α,
∴∠ADC=∠ADE+∠EDC=90°,
∴AD⊥BC.
∵AB=AC,
∴BD=CD;
②证明:∵AB=AC,∠ABC=α,
∴∠C=∠B=α.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,
∴∠DAC=α,
∴∠DAC=∠C.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
∴![]() .
.
故答案为:![]() .
.

 教学练新同步练习系列答案
教学练新同步练习系列答案