题目内容
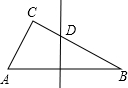 Rt△ABC中,∠C=90°,AB垂直平分线交直线BC于D,若∠DAB=2∠DAC,则∠B的度数是
Rt△ABC中,∠C=90°,AB垂直平分线交直线BC于D,若∠DAB=2∠DAC,则∠B的度数是
- A.18°
- B.36°
- C.54°
- D.30°
B
分析:根据垂直平分线性质易得∠B=∠DAB.运用三角形内角和定理解答.
解答: 解:∵D是AB垂直平分线上的点,
解:∵D是AB垂直平分线上的点,
∴DA=DB.
∴∠B=∠DAB.
∵∠DAB=2∠DAC,
∴3∠DAC+2∠DAC+90°=180°,
∠DAC=18°.
∴∠B=36°.
故选B.
点评:此题考查了线段垂直平分线的性质、三角形内角和定理等知识,属基础题.
分析:根据垂直平分线性质易得∠B=∠DAB.运用三角形内角和定理解答.
解答:
 解:∵D是AB垂直平分线上的点,
解:∵D是AB垂直平分线上的点,∴DA=DB.
∴∠B=∠DAB.
∵∠DAB=2∠DAC,
∴3∠DAC+2∠DAC+90°=180°,
∠DAC=18°.
∴∠B=36°.
故选B.
点评:此题考查了线段垂直平分线的性质、三角形内角和定理等知识,属基础题.

练习册系列答案
相关题目
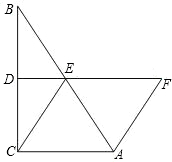 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形.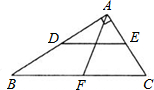 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=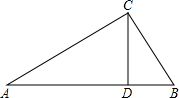 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD= 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为