题目内容
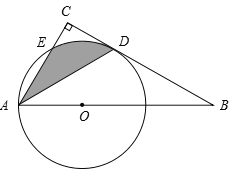
【题目】如图:在△ABC中,∠BAC =![]() ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.

【答案】证明见解析.
【解析】分析:根据三角形内角和定理求出∠B=∠CAD,根据角平分线性质求出AE=EF,由勾股定理求出AC=CF,证△ACG≌△FCG,推出∠CAD=∠CFG,得出∠B=∠CFG,推出GF∥AB,AD∥EF,得出平行四边形,根据菱形的判定判断即可.
详解:证明:∵AD⊥BC,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA),
∴AE=EF(角平分线上的点到角两边的距离相等),
∵CE=CE,∴由勾股定理得:AC=CF,
∵△ACG和△FCG中
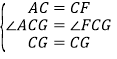
∴△ACG≌△FCG,
∴∠CAD=∠CFG,
∵∠B=∠CAD,
∴∠B=∠CFG,
∴GF∥AB,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
即AG∥EF,AE∥GF,
∴四边形AEFG是平行四边形,
∵AE=EF,
∴平行四边形AEFG是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目