题目内容
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;
(2)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.
(1)∵AB∥CD,
∴∠BAD+∠ADC=180,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180,
∴∠MAD+∠ADM=90,,
即AM⊥DM;
(2)作NM⊥AD交AD于N,
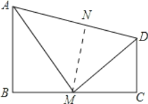
∵∠B=90,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,
即M为BC的中点.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目





