题目内容
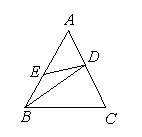
如图，已知AB∥CD，∠ACB=90°，E为AB的中点，CE=CD，DE与AC相交于F点.则DE、AC有怎样的关系？说明你的理由.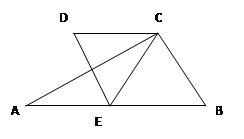
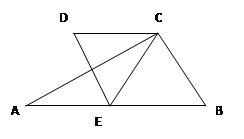
DE与AC互相垂直平分
DE与AC互相垂直平分；
∵已知，∠ACB=90°，E为AB的中点，
∴CE=AE=BE，
又已知AB∥CD，CE=CD，
∴CD=AE且AE∥CD，
连接AD，则得四边形AECD为平行四边形，
∵CE=CD，
∴四边形AECD为菱形，
∴DE与AC互相垂直平分．
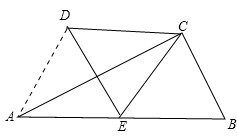
∵已知，∠ACB=90°，E为AB的中点，
∴CE=AE=BE，
又已知AB∥CD，CE=CD，
∴CD=AE且AE∥CD，
连接AD，则得四边形AECD为平行四边形，
∵CE=CD，
∴四边形AECD为菱形，
∴DE与AC互相垂直平分．
练习册系列答案
阅读快车系列答案
相关题目
