题目内容
【题目】在四边形 ABCD 中,BC=CD,连接 AC、BD,∠ADB=90°.
(1)如图 1,若 AD=BD=BC,过点 D 作 DF⊥AB 于点 F,交 AC 于点 E:
①求∠DAC;
②猜想 AE、DE、CE 的数量关系,并证明你的猜想;
(2)如图 2,若 AC=BD,求∠DAC 的度数.
【答案】(1)①![]() ,②
,②![]() ,证明见解析;(2)
,证明见解析;(2)![]()
【解析】
(1)①只要证明DA=DC,∠ADC=150°即可解决问题;
②结论:EC=ED+EA.如图1中,设AC交BD于点O,连接BE,在EC上截取EH=EB.由△EBD≌△HBC(SAS),推出DE=CH,可得EC=EH+CH=EB+ED=EA+ED解决问题;
(2)如图2中,作CK⊥BD于K,CH⊥AD交AD的延长线于H.首先证明四边形DHCK是矩形,再证明CH=![]() AC,即可解决问题;
AC,即可解决问题;
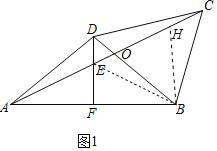
(1)①如图1中,
∵AD=BD=BC,BC=CD,
∴BD=BC=CD,
∴△BDC是等边三角形,
∴∠CDB=60°,
∵∠ADB=90°,
∴∠ADC=90°+60°=150°,
∵DA=DC,
∴∠DAC=∠DCA=15°,
②结论:EC=ED+EA.如图1中,设AC交BD于点O,连接BE,在EC上截取EH=EB.
∵DA=DB,DF⊥AB,
∴AF=FB,
∴EA=EB,
∴∠DAF=∠DBF,∠EAB=∠EBA,
∴∠DAE=∠DBE,
∵∠DAE=∠DCO,
∴∠DCO=∠OBE,
∵∠DOC=∠EOB,
∴∠BEO=∠ODC=60°,
∵EH=EB,
∴△EBH是等边三角形,
∴∠EBH=∠DBC=60°,BE=BH,
∴∠EBD=∠HBC,∵BD=BC,
∴△EBD≌△HBC(SAS),
∴DE=CH,
∴EC=EH+CH=EB+ED=EA+ED.
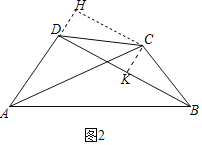
(3)如图2中,作CK⊥BD于K,CH⊥AD交AD的延长线于H.
∵∠H=∠CKD=∠HDK=90°,
∴四边形DHCK是矩形,
∴DK=CH,
∵CD=CB.CK⊥BD,
∴DK=![]() BD,
BD,
∵AC=BD,
∴CH=![]() AC,
AC,
在Rt△ACH中,sin∠CAD=![]() ,
,
∴∠CAD=30°.

【题目】为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
部分时段车流量情况调查表
时间 | 负责组别 | 车流总量 | 每分钟车流量 |
早晨上学6:30~7:00 | ①② | 2747 | 92 |
中午放学11:20~11:50 | ③④ | 1449 | 48 |
下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
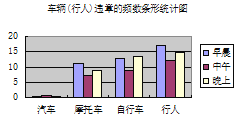
回答下列问题:
(1)请你写出2条交通法规.
(2)早晨.中午.晚上三个时段每分钟车流量的极差是多少,这三个时段的车流总量的中位数是多少.
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
(4)通过分析写一条合理化建议.